G. Mais alors la fenêtre ne sera plus
de forme et de taille constante, elle sera plus petite pour les pixels
proches du pourtour de la grille.
Un filtre spatial se base sur l'association à tout pixel p d'une fenêtre W(p), et ainsi pour une image I, on calcule en tout pixel p une certaine fonction des valeurs I(q) des pixels q dans la fenêtre W(p); cette fonction peut être une combinaison linéaire, la médiane, le minimum, le maximum, etc. ; le résultat donnera la valeur J(p) de p dans l'image filtrée J. Cette fenêtre est supposée de forme et de taille constante, par exemple un carré 3 × 3 ou 5× 5 ; en particulier pour les filtres linéaires, chaque fenêtre W(p) est le support d'un masque de coefficients positionné en p. On avait implicitement supposé que l'image de départ I est de support infini, c.-à-d. définie sur le plan discret Z2.
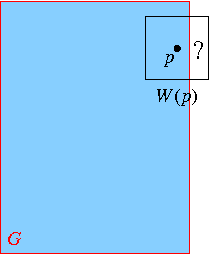
Cependant en pratique, toute image numérique est définie sur un support borné, généralement une grille rectangulaire G. Donc pour un pixel p proche du pourtour de G, la fenêtre W(p) peut dépasser en dehors de G, et les pixels de W(p) \ G n'ont pas de valeur dans l'image, donc le calcul de la fonction des valeurs dans W(p) n'est pas possible, cf. ci-contre.
Il y a essentiellement trois solutions à ce problème. La première tronque les fenêtres dépassant de la grille, les deux autres étendent l'image au-delà de la grille G, l'une sur tout le plan discret Z2, l'autre sur une bande entourant G.
L'idée la plus simple consiste à tronquer la
fenêtre, en enlevant de celle-ci la partie qui
dépasse de la grille. En d'autres termes, à tout
pixel p on associe la fenêtre
W(p) G. Mais alors la fenêtre ne sera plus
de forme et de taille constante, elle sera plus petite pour les pixels
proches du pourtour de la grille.
Cela marche bien pour les filtres basés sur un calcul du maximum ou du minimum des niveaux de gris dans la fenêtre (dilatation, érosion, gradient de Beucher, etc.), ou sur une comparaison du niveau de gris du pixel avec ce maximum et ce minimum (tel le filtre de Kramer et Bruckner). Mais pour les autres types de filtres, cela posera généralement des problèmes, par exemple :
On suppose qu'au-delà du pourtour de la grille, l'image se répète de façon périodique (comme par exemple une image utilisée comme texture de fond d'une page web). En d'autres termes, les coordonnées horizontale et verticale des pixels sont considérées comme circulaires, au-delà du bord droit on revient sur le bord gauche (et vice versa), au-delà du bord haut on revient sur le bord bas (et vice versa). Nous illustrons cela ci-dessous pour une image de la lettre R (la grille de départ G est indiquée, en position centrale) :
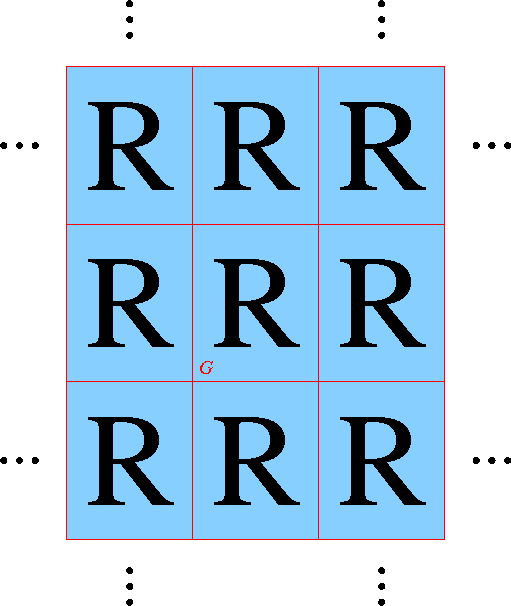
Cette approche est adaptée au filtrage en fréquences (filtre passe-bas, passe-haut ou passe-bande). En effet, l'analyse de fréquences d'une image discrète bornée est basée sur la Transformée de Fourier Discrète, qui calcule le spectre de fréquences d'une telle image. Cette transformée suppose l'espace périodique, les périodes horizontale et verticale correspondant aux dimensions de l'image ; d'ailleurs le calcul de celle-ci utilise des fonctions trigonométriques ayant ces périodes.
Pour les autres types de filtres, cette approche est artificielle. Par exemple, pour l'accentuation des arêtes, il y aura systématiquement un biais vers la détection d'arêtes sur le pourtour de la grille (d'ailleurs, si on périodise une image, on verra généralement une arête sur les bords séparant les différentes copies de l'image).
Il y a une variante, où on périodise l'image "en mirroir", chaque copie voisine est obtenue avec la symétrie par rapport au bord de la grille. Cela revient à périodiser comme plus haut une image formée de 4 copies symétriques de l'image de départ, comme illustré ci-dessous :
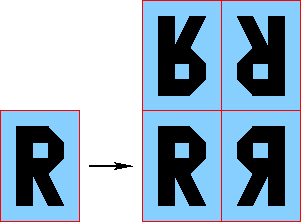
Ici la période est doublée, et il n'y aura plus de biais vers la détection d'arêtes sur le pourtour de la grille.
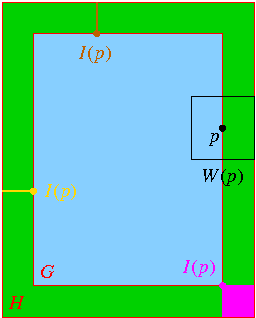
Ici on suppose, en l'absence de toute information sur le contenu de
l'image au-delà de la grille G, que les valeurs prises
par celle-ci sur le pourtour de G se prolongeront
au-delà. On entoure donc G par une bande H
suffisamment large pour que tout pixel p de G ait sa
fenêtre W(p) incluse
dans G 
H. Par
exemple si chaque fenêtre W(p) est un
carré (2n + 1) × (2n + 1)
centrée en p, alors H doit être
d'épaisseur n. L'image définie sur G
s'étendra alors sur H en attribuant à chaque
pixel de H celle du plus proche pixel de G. Donc la
valeur d'un pixel sur le bord gauche de G se transmettra aux
pixels de H sur sa gauche, et de même pour les bords
droit, haut et bas. La valeur d'un pixel sur un coin de G se
transmettra dans le rectangle de H selon les deux directions
des bords correspondants, comme illustré ci-contre (les
couleurs indiquent des zones de même valeur dans l'image) :
Cette solution a l'avantage de fonctionner pour tout type de filtre, et de ne pas introduire de biais notable. Notons en particulier que pour les filtres basés sur un calcul du maximum ou du minimum des niveaux de gris dans la fenêtre (dilatation, érosion, gradient de Beucher, etc.), ou sur une comparaison du niveau de gris du pixel avec ce maximum et ce minimum (comme le filtre de Kramer et Bruckner), cette approche donnera le même résultat que la troncature des fenêtres.
Une variante plus compliquée serait de faire sur H une extrapolation bilinéaire ou par splines de l'image sur G.
En conclusion, la meilleure solution est :