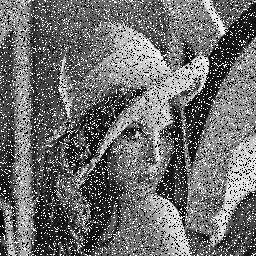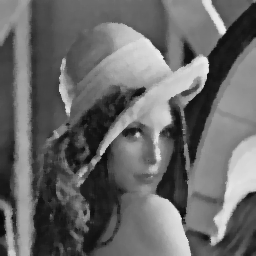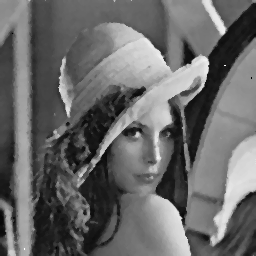Le filtre médian
Christian RONSE © (07/05/2008)
LSIIT UMR 7005 CNRS-ULP, Département d'Informatique de
l'ULP
La médiane est une mesure statistique qui
représente une alternative robuste à la
moyenne. Considérons n valeurs numériques
x1, ..., xn (pas
nécessairement distinctes), où n est
impair. On les ordonne de la plus petite à la plus
grande, ce qui donne la suite permutée
xi1, ...,
xin, où
{i1, ..., in} est une
permutation de {1, ..., n}. La médiane est alors la valeur
placée au milieu de cette suite ordonnée, à
savoir xim pour
m = (n+1)/2.
Par exemple, soit n = 9, et considérons les 9
valeurs
17, 1, 3, 5, 3, 1, 12, 2, 7.
Notons que certaines valeurs peuvent être
répétées, et qu'il ne faut pas supprimer les
répétitions ! En les ordonnant de la plus petite
à la plus grande, on obtient la suite
1, 1, 2, 3, 3, 5, 7, 12, 17.
La valeur au milieu de cette suite ordonnée est la 5ème,
à savoir 3, qui est donc la médiane des 9 valeurs.
On écrira med(x1, ...,
xn) pour la médiane des variables
x1, ..., xn. Ainsi
dans l'exemple ci-dessus, on a med(17,1,3,5,3,1,12,2,7) = 3. Notons
que - tout comme la moyenne - la médiane ne dépend pas
de l'ordre dans lequel sont données les n valeurs.
Le filtre médian est un filtre spatial qui calcule en chaque
pixel la médiane des niveaux de gris des pixels de sa
fenêtre, ce qui donnera le niveau de gris du pixel dans l'image
filtrée. Plus présisément, pour tout pixel
p, soit W(p) la fenêtre
associée à p ; on suppose que sa taille
|W(p)| est impaire (c'est ainsi le cas pour
une fenêtre centrée en p, par exemple une
fenêtre 3 × 3 ou 5 × 5). Etant donnée une
image I à niveaux de gris, le filtre médian
transformera I en une image J à niveaux de
gris, telle que pour tout pixel p, le niveau de gris
J(p) est la médiane des niveaux de
gris I(q) des pixels q dans la
fenêtre W(p) :
J(p) = med (I(q)
| q dans W(p)) .
Notons que ce calcul de J(p) se fait en parallèle, en d'autres termes le
calcul en un pixel p n'influe pas sur le calcul en un pixel
voisin q.
Pour comprendre le fonctionnement du filtre médian, on applique
le principe de dichotomie. Soit s une
intensité qu'on prendra comme seuil ; alors la
médiane de n variables x1, ...,
xn (n impair) sera 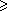 s si et seulement si la
majorité de ces n variables est
s si et seulement si la
majorité de ces n variables est  s. Donc si on appelle "clairs" les
niveaux de gris
s. Donc si on appelle "clairs" les
niveaux de gris  s, et
"sombres" ceux < s, le filtre médian
rendra un pixel "clair" ou "sombre" selon que la
majorité des pixels de la fenêtre autour de ce pixel sont
"clairs" ou "sombres".
s, et
"sombres" ceux < s, le filtre médian
rendra un pixel "clair" ou "sombre" selon que la
majorité des pixels de la fenêtre autour de ce pixel sont
"clairs" ou "sombres".
Vu que la médiane, en tant que mesure statistique,
représente une alternative à la moyenne, le filtre
médian constituera une forme de lissage qu'on peut utiliser
à la place du lissage linéaire. Les deux types de
filtres ont des propriétés différentes, qui selon
les cas peuvent donner l'avantage à l'un ou l'autre, comme nous
l'expliquerons ci-dessous. Pour une analyse plus
détaillée de ces propriétés, on se
reportera au document
complémentaire.
Non-création de nouveaux niveaux de gris
Une des propriétés fondamentales du filtre
médian, est qu'il ne crée pas de nouvelles valeurs de
niveaux de gris dans l'image. Trois conséquences importantes
sont que, contrairement au lissage
linéaire, ce filtre
- s'avère inutile pour créer des
dégradés dans une image dont les niveaux de gris ont
été sous-quantifiés.
- ne peut pas restaurer une image en demi-ton, au contraire il
accentuera l'effet de binarisation.
- peut s'appliquer aux images binaires (à deux valeurs), et
le résultat restera une image binaire.
En effet, la médiane de n variables est une de ces
variables. Aussi quand on applique le filtre médian à
une image I, la valeur de niveau de gris
J(p) obtenue en un pixel p (dans la
nouvelle image J) sera une des valeurs de niveaux de gris
I(q) (dans l'image de départ I) d'un
pixel q dans la fenêtre W(p) autour
de p. Par conséquent, l'ensemble des niveaux de gris
J(p) de la nouvelle image J sera inclus
dans celui des niveaux de gris I(p) de l'image de
départ I.
Il s'ensuit que dans une image ayant peu de niveaux de gris distincts,
l'application du filtre médian n'augmentera pas le nombre de
niveaux de gris, elle peut par contre le diminuer. Ainsi le filtre
médian est absolument inutile pour créer des
dégradés ou pour éliminer les faux contours
causés par la sous-quantification de niveaux de gris : des
niveaux de gris sous-quantifiés le resteront. Par exemple si on
quantifie sur 5 bits l'échelle de niveaux de gris de [0,255]
(qui nécessite 8 bits), cela revient à éliminer
les 3 bits les moins significatifs ; quant on ramène
à 8 bits l'échelle réduite, les 3 bits les moins
significatifs sont mis à 0, donc les niveaux de gris seront
tous multiples de 8, et l'application du filtre médian n'y
changera rien.
Par contre les filtres linéaires, qui créent de
nouvelles valeurs de niveaux de gris, peuvent être
utilisés pour générer des dégradés
et atténuer le phénomène de faux contours.
Considérons maintenant le comportement du filtre médian
sur une image binaire, soit à valeurs 0 et 1, soit à
deux niveaux de gris a0 et a1
(où a0 < a1). En
application du principe de dichotomie, la médiane de n
variables binaires x1, ...,
xn sera celle des deux valeurs (0,1 ou
a0, a1) qui est
majoritairement représentée parmi les n ;
en d'autres termes, l'opérateur de médiane
représente simplement un vote majoritaire parmi les variables
binaires. Donc le filtre médian attribuera à chaque
pixel la valeur majoritaire dans sa fenêtre.
Pour illustrer ce comportement, considérons par exemple l'effet
du filtre sur une image en demi-ton
(half-tone en anglais). Celle-ci ne comporte que des pixels
noirs et blancs, et l'intensité moyenne des pixels blancs et
noirs autour d'un point représente une approximation du niveau
de gris qu'aurait l'image à cet endroit (donc un lissage
linéaire ou flou devrait donner une approximation de l'image
à niveaux de gris correspondante, et effectivement on obtient
cet effet en regardant une telle image à une certaine
distance). Le processus pour engendrer une image en demi-ton à
partir d'une image à niveaux de gris s'appelle en anglais
dithering. Si le lissage linéaire restaure dans une
certaine mesure l'image de départ, ce n'est pas le cas pour le
filtre médian. Nous savons déjà qu'il ne
crée pas de nouveaux niveaux de gris, donc l'image
filtrée restera binaire (avec des pixels blancs ou noirs). En
fait, le filtre médian accentuera l'effet de binarisation,
comme nous l'expliquons ci-dessous.
Qualifions de clair ou sombre un niveau de
gris suivant qu'il est supérieur ou inférieur à
la moyenne entre blanc et noir. Alors :
- une zone claire de l'image de départ aura, dans l'image en
demi-ton, une majorité de pixels blancs à chaque
endroit, et le filtre médian appliqué à l'image
en demi-ton rendra cette zone blanche ;
- une zone sombre de l'image de départ aura, dans l'image en
demi-ton, une majorité de pixels noirs à chaque endroit,
et le filtre médian appliqué à l'image en
demi-ton rendra cette zone noire.
Donc le filtre médian appliqué à l'image en
demi-ton donnera à peu près la même chose qu'un seuillage de l'image à niveaux de
gris correspondante en prenant un seuil gris moyen (de valeur
égale à la moyenne entre celles de blanc et de
noir). C'est ce que nous illustrons ci-dessous pour une image à
niveaux de gris de 0 à 255 :
 |
|
 |
| Image originale. |
|
Image en demi-ton
obtenue par
"dithering". |
 |
|
 |
|
 |
Lissage linéaire 3 × 3
de
l'image en demi-ton. |
|
Application du filtre médian
3
× 3 sur l'image en demi-ton. |
|
Image originale seuillée
à
128. |
On peut ainsi utiliser le filtre médian si l'effet
recherché correspond à un seuillage de l'image
avant sa conversion en demi-ton.
Pratiquement pas de flou
Le filtre médian est réputé ne pas introduire de
flou dans les images. Ce n'est pas totalement vrai, il peut
étendre un dégradé présent le long d'une
arête courbe ou autour d'un coin, donnant donc un effet visuel
de léger flou, mais c'est sans commune mesure avec le flou
provoqué par le lissage linéaire.
Cela provient du fait que le filtre médian préserve les
marches et rampes rectilignes. Une marche représente
une augmentation abrupte du niveau de gris, tandis qu'une
rampe signifie une augmentation progressive et monotone du
niveau de gris. Une marche ou rampe est rectiligne si l'arête
qu'elle constitue dans l'image est rectiligne, en d'autres termes si
le niveau de gris est à peu près constant dans la
direction perpendiculaire à celle de l'augmentation.
Nous illustrons ci-dessous à gauche une marche et une rampe
rectilignes où le niveau de gris augmente de bas en
haut. Celles-ci seront préservées par le filtre
médian, à condition que le filtre utilise en chaque
pixel une fenêtre symétrique (par exemple 3
× 3 ou 5 × 5).
 |
|
 |
|
 |
|
 |
| Marche rectiligne. |
|
Rampe rectiligne. |
|
Damier avec un
flou 7 × 7. |
|
Résultat du filtre
médian
31 × 31. |
En ce qui concerne les arêtes non rectilignes, on remarquera que
le filtre médian peut déformer celles-ci. Pour une
arête courbe, le filtre médian érodera la zone
convexe bordée par l'arête, tandis qu'un coin sera
arrondi ou biseauté ; l'ampleur de la déformation
dépend de la taille de la fenêtre. Aussi quand cette
arête courbe ou ce coin présente un
dégradé, celui-ci verra sa surface agrandie, ce qui peut
donner une impression de flou. C'est ce que nous illustrons ci-dessus
à droite sur un damier légèrement flou,
traité par un filtre médian avec une très grande
fenêtre.
Elimination du bruit poivre et sel
Le bruit impulsif, aussi appelé bruit poivre et
sel, est une dégradation de l'image où certains
pixels deviennent aléatoirement soit blancs, soit noirs. On
suppose généralement que la probabilité qu'un
pixel devienne blanc (resp. noir) est constante sur l'image, et que le
devenir de chaque pixel est indépendant de celui des autres.
Contrairement au lissage linéaire, le filtre médian est
bien adapté au filtrage du bruit impulsif. Il s'appliquera
aussi pour éliminer des griffes dans une image. C'est ce que
nous illustrons dans les exemples ci-dessous. On remarquera que le
filtre médian de fenêtre 5 × 5 peut éliminer
certains détails qui seront préservés par celui
de fenêtre 3 × 3, mais que ce dernier laisse subsister une
partie du bruit, qui nécessitera pour être enlevé,
une 2ème, voire une 3ème application du filtre.
 |
|
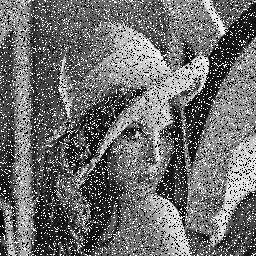 |
Image originale
(Lenna,
© Playboy). |
|
Image avec un bruit poivre et sel
affectant
25% des pixels. |
 |
|
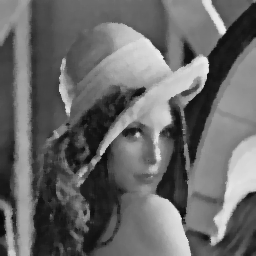 |
Lissage linéaire 5 × 5
de
l'image bruitée. |
|
Filtrage médian 5 × 5
de
l'image bruitée. |
 |
|
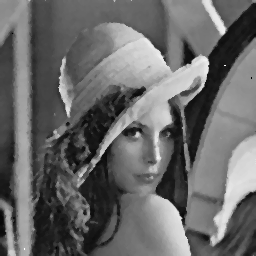 |
Filtrage médian 3 × 3
de
l'image bruitée. |
|
2ème application
du filtre
médian 3 × 3. |
 |
|
 |
| Image originale. |
|
Image avec des griffes
noires et
blanches. |
 |
|
 |
Application du filtre médian
5
× 5 sur l'image griffée. |
|
Filtre médian 3 × 3
appliqué
2 fois sur l'image griffée. |
On remarquera que le lissage linéaire n'élimine pas le
bruit poivre et sel, mais a plutôt tendance à
"l'étaler".
La bonne performance du filtre médian pour ce type de bruit
découle de la propriété de la médiane
d'être, contrairement à la moyenne, quasiment insensible
aux valeurs extrêmes. Mais cela suppose que la
probabilité qu'un pixel soit bruité "poivre"
(très sombre), et celle qu'il soit bruité
"sel" (très clair), sont toutes deux
inférieures à 1/2. Ainsi, on pourra supposer que
pour la plupart des pixels p, la fenêtre
W(p) ne contient qu'une minorité de pixels
"poivre", et de même pour "sel".
En effet, si la majorité des pixels de la fenêtre
W(p) autour d'un pixel p sont
bruités "poivre", c.-à-d. à niveau de
gris très bas, alors le filtre médian attribuera
à ce pixel un niveau de gris très bas, c.-à-d. le
pixel p sera bruité "poivre" dans l'image
filtrée. Il en sera de même pour une majorité de
pixels de la fenêtre bruités "sel",
c.-à-d. à niveau de gris très haut. Par contre,
si dans la fenêtre W(p) le nombre
nP de pixels bruités
"poivre" et le nombre nS de
pixels bruités "sel" sont tous deux <
|W(p)| / 2, alors la médiane des
niveaux de gris de la fenêtre ne sera ni "poivre" ni
"sel", mais une valeur non bruitée. Cela signifie que
dans l'image filtrée, le pixel p aura une valeur non
bruitée.
En ce qui concerne les autres types de bruit (comme le bruit
Gaussien), qui tendent à affecter un nombre plus important de
pixels, mais avec une amplitude moindre, il est parfois difficile de
départager les performances du filtre médian et du
lissage linéaire.
 |
|
 |
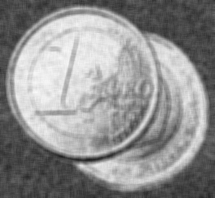
| Image originale. |
|
Image bruitée. |
 |
|
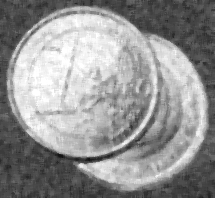 |
| Lissage linéaire 5 × 5 de
l'image bruitée. |
|
Filtrage médian 5 × 5 de l'image
bruitée. |
Dans l'exemple ci-dessus, comparé au lissage linéaire,
le filtre médian n'introduit pas de flou, préserve un
peu mieux les détails, mais laisse le bruit un peu plus
visible.
Retour à l'index
 s si et seulement si la
majorité de ces n variables est
s si et seulement si la
majorité de ces n variables est 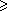 s. Donc si on appelle "clairs" les
niveaux de gris
s. Donc si on appelle "clairs" les
niveaux de gris 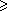 s, et
"sombres" ceux < s, le filtre médian
rendra un pixel "clair" ou "sombre" selon que la
majorité des pixels de la fenêtre autour de ce pixel sont
"clairs" ou "sombres".
s, et
"sombres" ceux < s, le filtre médian
rendra un pixel "clair" ou "sombre" selon que la
majorité des pixels de la fenêtre autour de ce pixel sont
"clairs" ou "sombres".