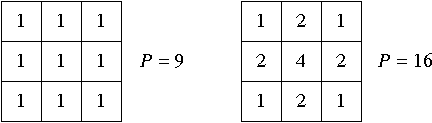
Supposons des images dont les niveaux de gris s'étendent dans l'intervalle [A,B], où A < B (typiquement, [0,255] pour les images affichées sur les écrans des ordinateurs). Si on filtre une telle image par convolution ou corrélation avec un masque, les valeurs résultantes n'appartiendront plus nécessairement à cet intervalle. Cela ne pose pas de problème si ce filtrage a pour but de faire une mesure sur l'image en vue d'une décision (par example une accentuation des arêtes, en vue de la localisation de celles-ci, c.-à-d. de l'extraction d'une image binaire des arêtes à partir de l'image accentuée). Par contre, si l'on veut afficher l'image filtrée, il convient de contrôler les valeurs d'intensité obtenues sur les pixels.
Soient P la somme des coefficients positifs du masque, et -N la somme de ses coefficients négatifs. Donc P et N sont non-négatifs. Pour obtenir la valeur la plus élevée possible dans la convolution, il faut que les coefficients positifs du masque se positionnent sur les intensités les plus élevées de l'image, et que les coefficients négatifs se positionnent sur les intensités les plus basses. Donc la valeur maximum obtenue par la convolution sera PB - NA. Inversément, pour obtenir la valeur la plus basse possible dans la convolution, il faut que les coefficients positifs du masque se positionnent sur les intensités les plus basses de l'image, et que les coefficients négatifs se positionnent sur les intensités les plus élevées. Donc la valeur minimum obtenue par la convolution sera PA - NB. On obtient ainsi l'intervalle de valeurs [PA - NB,PB - NA] dans l'image filtrée ; cet intervalle est de largeur (P + N)(B - A), contre B - A dans l'image de départ. Par exemple, pour [A,B] = [0,255], on obtiendra l'intervalle [-255N,255P].
L'opération sur les intensités à effectuer sur l'image filtrée dépend du type de filtrage: lissage, accentuation, rehaussement, accentuation des arêtes.
Ici P = 1 et N = 0, donc l'intervalle de valeurs [A,B] est préservé. D'ailleurs, le lissage calcule en tout point une moyenne pondérée des valeurs dans son voisinage, et une telle opération donne toujours un résultat appartenant à l'intervalle des valeurs de départ. Donc ici il n'y a rien à faire.
On définit parfois des masques de lissage avec P > 0, mais pas nécessairement égal à 1. Ainsi on peut remplacer des coefficients fractionnaires par des entiers, en multipliant chaque coefficient par le dénominateur commun, qui donne la nouvelle valeur de P. Par exemple, les masques de lissage vus précédemment deviennent :
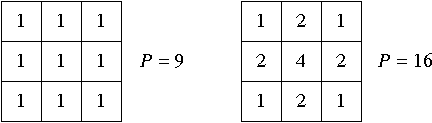
Alors on divisera le résultat de la convolution par P. Ainsi en chaque point on évite d'utiliser des fractions dans le calcul de la convolution, on ne fait qu'une division à la fin. On avait procédé de même pour les masques de chanfrein, en particulier ceux de Borgefors, pour le calcul des distances.
Ici P = N > 0, et généralement P < 1. Donc l'intervalle de valeurs devient [P(A - B),P(B - A)]. Par exemple, pour [A,B] = [0,255], cela donne [-255P,255P].
Nous avons vu que l'accentuation donne un résultat nul sur les zones de l'image où le niveau de gris est constant, mais une alternance de valeurs négatives et positives sur une arête. On a donc deux options d'affichage :
On obtient typiquement un tel rehaussement en additionnant l'image et
l'accentuation (éventuellement pondérée par un
facteur). Ici les zones de l'image à niveau de gris constant
sont préservées. Il importe de les préserver
encore après normalisation, donc on ne peut pas modifier les
valeurs incluses dans l'intervalle [A,B]. On va donc
simplement tronquer les valeurs dépassant l'intervalle, ce qui
donne la transformation de niveaux de gris :
g -> B
si g > B,
g -> A
si g < A,
g -> g
sinon.
Comme dans l'accentuation, on a P = N > 0, et on
obtient l'intervalle [P(A
- B),P(B - A)]. Ici le signe de la
convolution dépend de l'angle entre les orientations du masque
et de l'arête, et une rotation d'un demi-tour fait changer de
signe la convolution. Donc seule la valeur absolue de celle-ci compte
pour l'affichage, et on applique ainsi la transformation de niveaux de
gris
g -> A + |g|/P.
Pour l'opérateur de Sobel, on prend la combinaison quadratique
sqrt(gx2 +
gy2) des
valeurs gx
et gy des convolutions par les deux
masques ; celle-ci appartiendra à l'intervalle
[0,sqrt(2)P(B - A)], et on lui appliquera
la transformation de niveaux de gris
g -> A + g/sqrt(2)P.