| J(p) = | maxp | si I(p) | 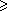 |
(maxp + minp)/2, |
| minp | si I(p) | < | (maxp + minp)/2. |
Le filtre de Kramer et Bruckner, introduit en 1975, est le premier d'une famille de filtres non-linéaires qu'on appelle des filtres de choc. Leur effet est le contraire de celui du lissage, ils réduisent l'étendue des dégradés. Ils opèrent en étendant les minima et maxima de niveaux de gris dans une image. En répétant l'application d'un tel filtre, on aboutit à une image sans le moindre dégradé, donc formée de zones constantes séparées par des marches abruptes.
Décrivons ce filtre. On suppose qu'à tout pixel p on associe une fenêtre W(p). Alors le filtre de Kramer et Bruckner transforme une image à niveaux de gris I en une nouvelle image à niveaux de gris J définie comme suit. Pour tout pixel p, posons :
minp = min (I(q) | q dans W(p)), maxp = max (I(q) | q dans W(p)) ;
alors J(p) est donné par
J(p) = maxp si I(p) (maxp + minp)/2, minp si I(p) < (maxp + minp)/2.
En d'autres termes, on compare le niveau de gris I(p) avec le maximum maxp et le minimum minp des niveaux de gris de la fenêtre ; suivant que I(p) est plus proche de maxp (c.-à-d. I(p) > (maxp + minp)/2) ou de minp (c.-à-d. I(p) < (maxp + minp)/2), on pose J(p) = maxp ou minp ; si I(p) est équidistant de maxp et de minp (c.-à-d. I(p) = (maxp + minp)/2), on choisit J(p) = maxp. Ce dernier choix implique que le filtre n'est pas auto-dual ; dans le cas de l'équidistance, le dual du filtre aurait choisi J(p) = minp.
Le filtre de Kramer et Bruckner préserve toute zone de l'image où le niveau de gris est constant. Il en va de même pour toute zone ayant exactement deux niveaux de gris. En particulier, l'application de ce filtre à une image binaire ne modifiera pas celle-ci.
Dans une zone de variation de niveaux de gris, ce filtre aura le comportement contraire du lissage linéaire, il réduira l'étendue des dégradés. Nous l'illustrons ci-dessous sur le profil de niveaux de gris le long d'une coupe perpendiculaire à une arête formant un dégradé :
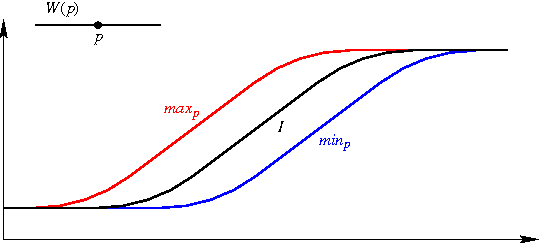
En haut à gauche, la fenêtre W(p)
centrée sur le point p.
En noir, le profil de l'image de départ I.
Les profils de maxp et
de minp respectivement en rouge et en
bleu.
En vert, le profil de l'image filtrée J.
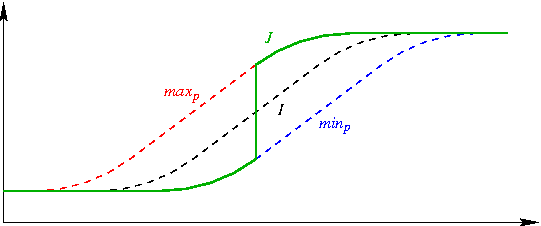
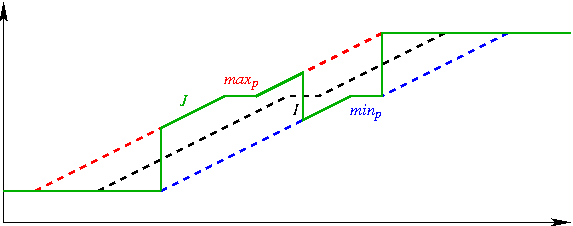
Quand la montée de niveaux de gris du dégradé est irrégulière ou interrompue par des paliers, le filtre peut produire une altenance de montées et de descentes, comme le montre l'exemple ci-dessous; :
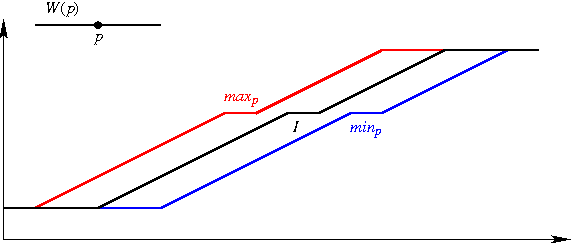
(Mêmes conventions que plus haut concernant W(p), I, maxp, minp et J.)
Il a été montré que pour une image dont les valeurs sont constantes en dehors d'un support borné, l'application répétée du filtre de Kramer et Bruckner aboutit après un nombre fini d'itérations à une image qui ne sera plus modifiée par ce filtre. Une telle image sera formée de zones constantes séparées par des marches abruptes.
Nous donnons ci-dessous quelques exemples d'applications répétées (jusqu'à convergence) du filtre, avec des fenêtres 3 × 3 ou 7 × 7. Ces expérimentations sont dues à Sébastien Lefèvre.
Considérons d'abord des objets noirs sur fond blanc, dont le bord forme un dégradé :
 |
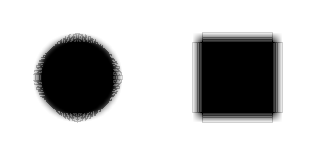 |
|
| Image originale. | Filtre 3 × 3 appliqué 1 fois. | |
 |
 |
|
| Filtre 3 × 3 appliqué 2 fois. | Filtre 3 × 3
répété jusqu'à convergence. |
|
 |
 |
|
| Filtre 7 × 7 appliqué 1 fois. | Filtre 7 × 7
répété jusqu'à convergence. |
 |
 |
 |
||
| Image originale. | Filtre 3 × 3 appliqué 1 fois. |
Filtre 3 × 3 appliqué 10 fois. |
||
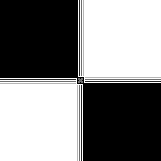 |
 |
 |
||
| Filtre 3 × 3
répété jusqu'à convergence. |
Filtre 7 × 7 appliqué 1 fois. |
Filtre 7 × 7 appliqué 2 fois. |
||
| (La 3ème application du filtre 7 × 7 ne modifie plus l'image.) | ||||
Le fait vu plus haut que sur un dégradé le filtre peut produire une alternance de montées et de descentes de niveaux de gris, induit qu'en répétant le filtre, on pourra obtenir des stries là où se trouvaient les dégradés.
Considérons ensuite des images naturelles. On remarquera que la répétition du filtre jusqu'à convergence produira une image avec des arêtes et de larges zones à niveau de gris constant. L'épaisseur des lignes d'arête est à la mesure de la taille de la fenêtre.
En conclusion, pour rehausser une image, il vaut mieux n'appliquer le filtre qu'une seule fois. La répétition du filtre produira plutôt une simplification de l'image.
 |
 |
|
| Image originale. | Filtre 3 × 3 appliqué 1 fois. | |
 |
 |
|
| Filtre 3 × 3 appliqué 2 fois. | Filtre 3 × 3 appliqué 5 fois. | |
 |
 |
|
| Filtre 3 × 3
répété jusqu'à convergence. |
Filtre 7 × 7 appliqué 1 fois. | |
 |
 |
|
| Filtre 7 × 7 appliqué 2 fois. | Filtre 7 × 7
répété jusqu'à convergence. |
 |
 |
|
| Image originale (Lenna, © Playboy). |
Filtre 3 × 3 appliqué 1 fois. | |
 |
 |
|
| Filtre 3 × 3 appliqué 2 fois. | Filtre 3 × 3
répété jusqu'à convergence. |
|
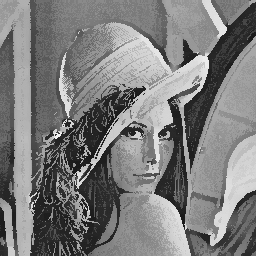 |
 |
|
| Filtre 7 × 7 appliqué 1 fois. | Filtre 7 × 7
répété jusqu'à convergence. |