 |
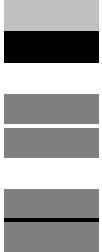 |
|
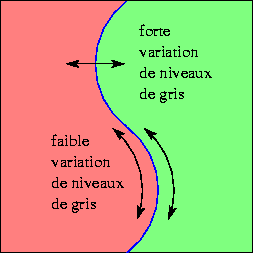
| Variation des niveaux de gris, faible le long de l'arête, forte perpendiculairement. |
Marche, ligne claire, ligne sombre. |
Une arête est une ligne visible dans l'image, située à la séparation entre deux zones de l'image. Quand cette ligne est fermée, l'arête correspond à un contour, c.-à-d. à la frontière d'un objet présent dans l'image. Le long de l'arête, le niveau de gris change peu, par contre il change fortement dans une coupe perpendiculaire à celle-ci. Par exemple, une arête verticale correspond à une variation rapide des niveaux de gris dans la direction horizontale. C'est ce que nous illustrons dans le schéma ci-dessous à gauche (où les couleurs ne représentent pas des niveaux de gris, mais désignent les deux côtés de l'arête) :
 |
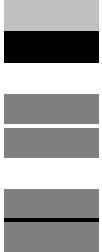 |
|
| Variation des niveaux de gris, faible le long de l'arête, forte perpendiculairement. |
Marche, ligne claire, ligne sombre. |
Une arête de type marche est une séparation abrupte entre deux zones relativement homogènes de niveaux de gris différents ; dans la direction perpendiculaire à celle-ci, le profil de niveaux de gris forme un saut brusque. Un autre type d'arête est une ligne, claire ou sombre, séparant deux zones relativement homogènes de niveaux de gris assez semblables. L'image ci-dessus à droite montre de haut en bas une marche, une ligne claire et une ligne sombre, toutes trois horizontales.
La détection d'arêtes a pour objet de localiser les arêtes dans une image. Dans l'approche traditionnelle basée sur des filtres, elle implique deux étapes :
La figure ci-dessous illustre les deux étapes de la détection d'une arête marche à travers le profil de niveaux de gris d'une coupe perpendiculaire à cette arête :
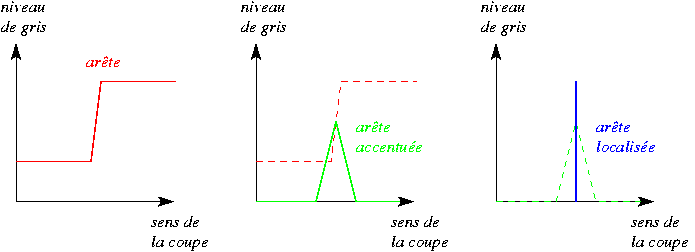
Nous ne traiterons ici que de la première étape, et nous nous restreindrons aux arêtes de type marche.
Un filtre linéaire d'accentuation utilisant un masque symétrique aura généralement une réponse non-nulle sur une arête, mais nulle sur une zone à niveau de gris constant. En prenant la valeur absolue de cette réponse, on accentuera les arêtes. Cependant un tel filtre n'est pas assez spécifique, il réagira également sur du bruit, des pics isolés, etc.
On se basera donc sur le fait qu'une arête marche sépare deux zones dont les niveaux de gris moyens sont différents, et c'est cette différence qu'on mesurera.
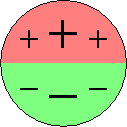
On prendra donc un masque de corrélation orienté, avec des coefficients positifs d'un côté et négatifs de l'autre. Un tel masque M sera anti-symétrique : pour tout pixel q de son support S, on a M(-q) = - M(q). L'orientation du masque est donnée par un axe dont les côtés positifs et négatifs coïncindent avec les coefficients positifs et négatifs. Le masque sera symétrique par rapport à cet axe, et anti-symétrique par rapport à l'axe perpendiculaire :
 |
 |
|
| Masque orienté positif en haut, négatif en bas. |
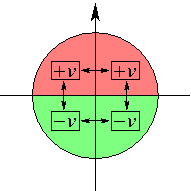
Axe d'orientation du masque et axe orthogonal d'anti-symétrie. |
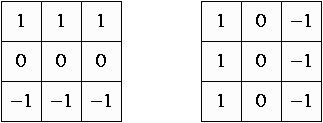
Les exemples les plus simples sont les masques de Prewitt, nous montrons ci-dessous les deux masques pour les orientations nord (vers le haut) et ouest (vers la gauche) ; on n'a alors pas besoin des masques pour les orientations sud (vers le bas) et est (vers la droite), car ils sont obtenus par changement de signe des coefficients, donc il suffit de changer le signe de la corrélation.
Considérons la réponse de la corrélation avec un tel masque. Comme il est anti-symétrique, la somme de ses coefficients est nulle, donc cette réponse est nulle sur une zone à niveau de gris constant. Il n'y aura donc de réponse significative que sur les zones de variation. Ce sera le cas pour un pic ou du bruit, mais la réponse sera assez faible ; en effet chaque moitié (positive et négative) du masque correspond à un lissage, et ainsi le masque mesure la différence de niveau de gris moyen entre les deux côtés, ce qui a tendance à amoindrir les variations isolées.
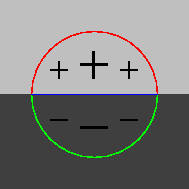
Donc la réponse de la corrélation avec le masque sera plus conséquente au voisinage d'une arête marche. Nous orientons celle-ci dans le sens de croissance des niveaux de gris (donc perpendiculairement à la direction de la ligne d'arête). La réponse de la corrélation variera suivant la position du pixel par rapport à l'arête, et l'angle entre l'orientation du masque et celle de l'arête.
Supposons d'abord le pixel sur l'arête. Si le masque est orienté dans le même sens que l'arête, il y aura superposition des coefficients positifs du masque avec les niveaux de gris clairs de l'arête, et des coefficients négatifs avec les niveaux de gris sombres, donc la réponse sera un multiple de la différence entre les niveaux de gris clairs et sombres, c.-à-d. fortement positive. Au fur et à mesure que leurs orientations s'éloignent, le nombre de coefficients positifs décroîtra du côté clair de l'arête et croîtra du côté sombre, tandis que le nombre de coefficients négatifs croîtra du côté clair et décroîtra du côté sombre ; donc la réponse diminuera. Quand leurs orientations sont perpendiculaires, les coefficients positifs et négatifs se compensent de chaque côté de l'arête, donc la réponse sera nulle. Ensuite, quand l'angle entre les deux orientations devient obtus, le réponse deviendra négative. Finalement, pour des orientations opposées du masque et de l'arête, on obtiendra l'opposé de la situation où ces orientations coïncidaient, donc la réponse sera fortement négative.
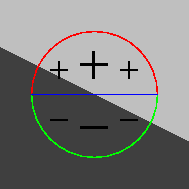
| Orientation de l'arête et du masque |
 |
 |
||
| alignées : forte réponse positive. |
en angle aigu : faible réponse positive. |
|||
 |
 |
 |
||
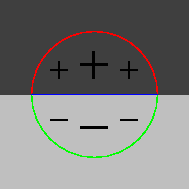
| orthogonales : réponse nulle. |
en angle obtus : faible réponse négative. |
opposées : forte réponse négative. |
Considérons maintenant la variation de cette réponse en fonction de la position du pixel par rapport à l'arête. Si le masque est entièrement du même côté de l'arête, la réponse sera nulle. Quand le pixel se rapproche de l'arête, un nombre croissant de paires de pixels opposés dans le masque se retrouveront les positifs d'un côté de l'arête et les négatifs de l'autre côté, contribuant ainsi à donner un fort coefficient à la différence de niveaux de gris entre les deux côtés, donc la réponse croîtra en valeur absolue. La réponse sera la plus forte (en valeur absolue) lorsque le pixel est sur l'arête.
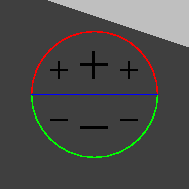
| Position du pixel et du masque par rapport à l'arête |
 |
 |
||
| masque du côté sombre de l'arête : réponse nulle. |
pixel du côté sombre, masque intersectant l'arête : réponse faible. |
|||
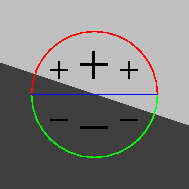 |
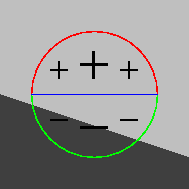 |
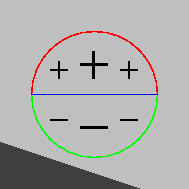 |
||
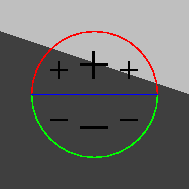
| pixel sur
l'arête : réponse la plus forte. |
pixel du côté clair, masque intersectant l'arête : réponse faible. |
masque du côté clair de l'arête : réponse nulle. |
En résumé, en prenant la valeur absolue de la corrélation avec le masque, on accentuera partiellement les arêtes marches : on obtiendra une valeur nulle sur une zone homogène mais positive le long d'une arête, d'autant plus forte que le pixel est proche de l'arête et que l'orientation de l'arête est parallèle à celle du masque (dans le même sens ou le sens opposé).
Il est donc possible d'accentuer les arêtes de n'importe quelle orientation en prenant des masques dans un grand nombre d'orientations : on fera la corrélation avec tous les masques, et en tout pixel on prendra les valeurs absolues des réponses, puis on sélectionnera la plus forte d'entre elles. Notons que pour deux orientations opposées, les masques correspondants ont des coefficients opposés, donc leurs corrélations seront de signe opposé mais de même valeur absolue ; on peut donc n'utiliser qu'un seul des deux masques, et limiter les orientations à un intervalle de 180°.
Par exemple, pour un masque 3 × 3 comme les masques de Prewitt, on peut avoir, en plus des orientations horizontales et verticales, celles en diagonales. Nous illustrons ci-dessous de tels masques pour les orientations nord-ouest et sud-ouest (ceux pour les orientations opposées sud-est et nord-est sont obtenus par changement de signe).
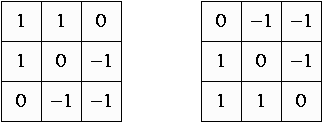
Sobel a donné une des premières méthodes d'accentuation des arêtes. Elle se base sur deux masques orientés selon les directions verticale et horizontale respectivement, assez semblables à ceux de Prewitt. La différence tient en l'introduction des coefficients 2 et -2, qui permettent d'avoir une meilleure réponse sur une arête oblique ou courbe.
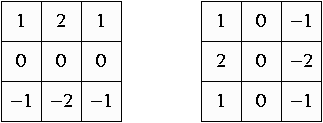
Sur une arête horizontale ou verticale, la corrélation avec ces deux masques donnera une réponse forte pour l'un et nulle pour l'autre. Pour une arête oblique, les deux réponses seront non-nulles mais assez faibles. On peut alors avoir une valeur forte dans tous les cas (arête horizontale, verticale ou oblique) en prenant la racine carrée de la somme des carrés des deux réponses.
Il y a une justification mathématique à ce choix de la combinaison quadratique des deux réponses. Etant donnée une fonction f à deux variables, la pente de celle-ci en un point p est donnée par un vecteur appelé le gradient, égal à (fx(p),fy(p)), où fx et fy désignent les dérivées partielles de f en x et y ; la longueur du gradient (l'amplitude de la pente) en p vaut donc (fx(p)2 + fy(p)2)1/2. On peut considérer la corrélation de l'image avec chacun des deux masques comme une approximation discrète de la dérivée de celle-ci (vue comme fonction) par rapport aux deux axes de coordonnées.
On pourrait aussi prendre comme combinaison la somme des valeurs absolues des réponses des deux corrélations. Il est également possible d'appliquer la méthode de Sobel avec les masques de Prewitt. Nous illustrons ci-dessous le détecteur d'arête de Sobel : les valeurs absolues des deux convolutions et leur combinaison quadratique.
 |
 |
|
| Image originale. | valeur absolue de la corrélation avec le masque nord. |
|
 |
 |
|
| valeur absolue de la corrélation avec le masque ouest. |
combinaison quadratique des deux. |
Notons finalement que le détecteur de Sobel, tout comme tout autre filtre d'accentuation de marches utilisant un petit masque, réagira à une arête de type ligne comme s'il s'agissait d'une succession rapprochée de deux marches, l'une montante et l'autre descendante. Donc les deux bords de la ligne, et non pas son centre, seront accentués.