M(q)  0 pour
tout q
0 pour
tout q  S , et
S , et
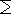 q
q
 S
M(q) = 1 .
S
M(q) = 1 .
Nous allons considérer ici certaines formes parmi les plus courantes de filtres linéaires. Ceux-ci pourront ensuite être comparés à des filtres non-linéaires ayant la même fonctionnalité (par exemple le lissage linéaire avec le filtre médian).
Comme les masques que nous utilisons sont symétriques, on peut indifféremment prendre la convolution ou la corrélation pour réaliser le filtre. Soit M un masque de support S contenant l'origine 0.
Le lissage est une opération fondamentale en traitement d'images, elle vise à atténuer ou supprimer les aspérités et petits détails dans une image.
Un masque de lissage M a ses coefficients non-négatifs, et la somme de ceux-ci vaut 1 :
M(q)
0 pour tout q
S , et
q
S M(q) = 1 .
En d'autres termes, la corrélation de l'image avec le masque M remplace (en parallèle) le niveau de gris de chaque pixel par une moyenne pondérée de ceux de son voisinage Sp.
Nous illustrons ci-dessous deux masques de lissage à support 3 × 3. Le premier a ses coefficients constants (donc il applique aux niveaux de gris une moyenne non pondérée), tandis que le second voit ses coefficients diminuer du centre à la périphérie.
En général, les coefficients d'un masque de lissage peuvent être donnés manuellement, ou par une fonction mathématique, par exemple la Gaussienne (cloche de Gauss) définie par :
L'effet du lissage est de "mélanger" les niveaux de gris dans un voisinage, donc d'engendrer du flou sur l'image. C'est ce que nous illustrons ci-dessous pour des masques de lissage n × n à coefficients constants (tous égaux à 1 / n2), pour n croissant :
 |
 |
|
| Image originale. | Lissage linéaire 3 × 3 de l'image. | |
 |
 |
|
| Lissage linéaire 7 × 7 de l'image. | Lissage linéaire 15 × 15 de l'image. |
En particulier certains détails de l'image peuvent être éliminés (comme la texture des cheveux et de la moustache d'Einstein). Aussi dans certaines circonstances, un léger lissage (avec un masque 3 × 3 par exemple) peut être utilisé pour améliorer l'aspect esthétique d'une image.
Cet effet de flou, qui augmente avec la taille du masque, se manifeste spécialement dans les zones à forte variation de niveaux de gris, comme les arêtes. Nous illustrons ci-dessous le profil de niveaux de gris le long d'une coupe perpendiculaire à une arête de type "marche", et ce qu'il devient après lissage : la transition devient progressive, ce qui se correspond visuellement au flou :
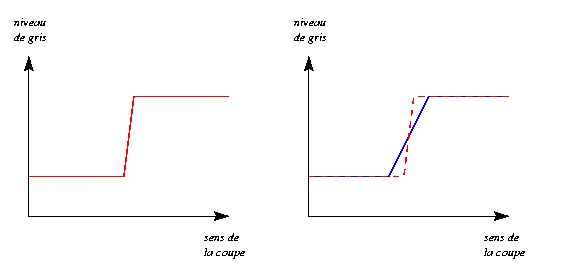
A gauche, le profil de niveaux de gris de la marche dans le sens
perpendiculaire à l'arête (en rouge) ;
a droite, le profil de la marche après lissage (en bleu, et en
pointillés en rouge : le profil original).
Comme la somme des coefficients du masque vaut 1, le lissage préservera toute zone de l'image où le niveau de gris est constant. Par conséquent son comportement, qui conserve les zones à faibles variations de niveaux de gris mais supprime les variations rapides, s'apparente à celui d'un filtre passe-bas en traitement du signal (un tel filtre annule les hautes fréquences et préserve les basses fréquences dans l'image).
Outre l'élimination de petits détails, le lissage linéaire peut s'avérer utile dans certaines circonstances, par exemple :
Nous illustrons ci-dessous ces applications. Tout d'abord, dans le cas du bruit, comme les changements qu'il induit sur les niveaux de gris des différents pixels ne sont pas corrélés, la moyenne de ces niveaux de gris tendra à atténuer le bruit. Nous montrons ci-dessous l'effet du lissage linéaire (et par comparaison, celui du filtre médian) sur une image corrompue par du bruit Gaussien (c.-à-d. dont chaque pixel voit son niveau de gris modifié par ajout d'une valeur aléatoire dont la distribution de probabilité suit la loi de Gauss) :
 |
 |
|
| Image bruitée. | Lissage linéaire 3 × 3
de l'image bruitée. |
|
 |
 |
|
| Lissage linéaire 5 × 5
de l'image bruitée. |
Filtrage médian 5 × 5
de l'image bruitée. |
Nous illustrons ensuite l'effet du lissage linéaire sur une image dont les niveaux de gris ont été sous-quantifiés. Un dégradé progressif de niveaux de gris devient alors une succession de sauts, et on souhaite atténuer cet effet en recréant un tel dégradé. Ici le filtre médian s'avère inutile, car il ne crée pas de nouvelles valeurs de niveaux de gris, donc pas de dégradés. Le flou du lissage crée un dégradé sur les arêtes (tant sur les vrais contours des objets que sur les faux dus à la sous-quantification) :
 |
 |
|
| Image originale (Lenna, © Playboy). |
Image sous-quantifiée à 16 niveaux de gris. |
|
 |
 |
|
| Lissage linéaire 3 × 3
de l'image sous-quantifiée. |
Lissage linéaire 5 × 5
de l'image sous-quantifiée. |
Dans le cas de la détection d'arêtes, un lissage linéaire préalable a plusieurs effets, qui peuvent aussi être obtenus par un filtre médian :
C'est ce que nous illustrons ci-dessous pour un filtre d'extraction d'arêtes appliqué à l'image d'Einstein, en versions originale et bruitée, avec ou sans lissage :
 |
 |
|
| Extraction d'arêtes sur l'image originale. |
Extraction d'arêtes sur l'image lissée 5 × 5. |
|
 |
 |
|
| Extraction d'arêtes sur l'image bruitée. |
Extraction d'arêtes sur l'image bruitée lissée 5 × 5. |
Considérons enfin l'effet du lissage sur une image en demi-ton (half-tone en anglais). Une telle image ne comporte que des pixels noirs et blancs, et l'intensité moyenne des pixels blancs et noirs autour d'un point représente une approximation du niveau de gris qu'aurait l'image à cet endroit. Le processus pour engendrer une image en demi-ton à partir d'une image à niveaux de gris s'appelle en anglais dithering, il descend des procédés utilisés autrefois pour imprimer des images à niveaux de gris avec de l'encre noire sur papier blanc, et plus tard pour l'affichage de niveaux de gris sur des écrans d'ordinateurs dont les pixels ne pouvaient prendre que les intensités noir ou blanc. Le filtre médian n'est d'aucune utilité sur une image en demi-ton. Par contre un lissage linéaire, qui opère une moyenne locale des intensités dans l'image, donne une bonne approximation de l'image à niveaux de gris correspondante :
 |
 |
 |
||
| Image originale. | Image en demi-ton obtenue par "dithering". |
Lissage linéaire 3 × 3 de l'image en demi-ton. |
L'accentuation (en anglais : sharpening) consiste à soustraire l'image lissée de l'image originale. On calcule donc, pour une image I et un masque de lissage M :
I - (M o I) .
Comme I = i * I = i o I pour l'impulsion i, cela revient en fait à corréler l'image avec i - M. En supposant un espace discret, c.-à-d. E = Zn, i - M sera le masque M# de même support S que M, prenant les valeurs :
M#(0) = 1 - M(0) et
M#(q) = - M(q) pour qS \ {0} .
De façon équivalente, on définit M# comme un masque de support S contenant l'origine, tel que
0
M#(0)
1 ,
M#(q)0 pour tout q
S \ {0} , et
q
S M(q) = 0 .
Nous illustrons ci-dessous les deux masques d'accentuation à support 3 × 3 dérivés des deux masques de lissage donnés plus haut :
L'accentuation est apparentée à la version discrète du Laplacien. Dans un espace continu, c.-à-d. E = Rn, le Laplacien est l'opérateur transformant une fonction en la somme de ses dérivées secondes par rapport à chacune de ses variables :
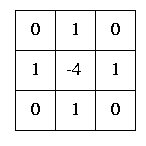
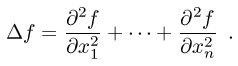
Dans le cas discret (E = Zn), on peut approximer la dérivé première f'(x) par f(x+1) - f(x), et la dérivé seconde f"(x) par celle de f'(x) - f'(x-1), c.-à-d. par f(x+1) - 2f(x) + f(x-1), alors dans le plan discret (E = Z2) le Laplacien correspond à la corrélation par le masque ci-contre.
Dans le cas d'une arête de type "marche", l'accentuation donnera un effet d'arête entre deux zones de valeur quasi-nulle, comme illustré ci-dessous :
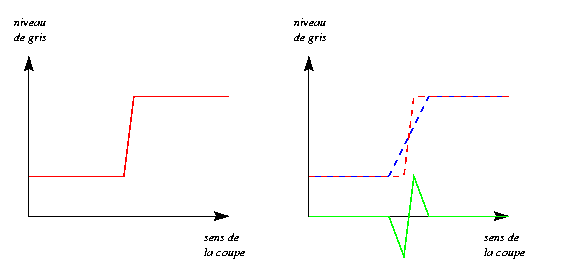
A gauche, le profil de niveaux de gris de la marche dans le sens
perpendiculaire à l'arête (en rouge) ;
A droite, le profil de la marche après accentuation (en vert),
et en pointillés :
le profil original (en rouge) et celui de l'arête lissée
(en bleu).
Comme la somme des coefficients du masque vaut 0, l'accentuation donnera la valeur 0 sur toute zone de l'image où le niveau de gris est constant. Son comportement s'apparente ainsi à celui d'un filtre passe-haut en traitement du signal (un tel filtre annule les basses fréquences et préserve les hautes fréquences dans l'image).
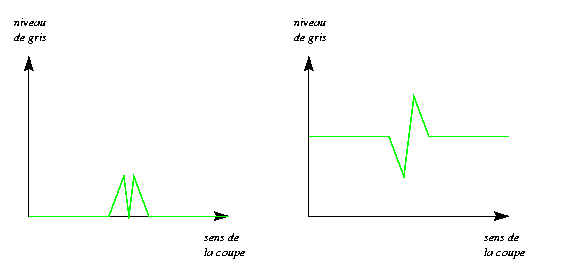
L'accentuation d'une image donnera des valeurs positives et négatives. On peut le visualiser en niveaux de gris en transformant ces valeurs :
C'est ce que nous illustrons ci-dessous pour l'accentuation de l'arête "marche" :
Si on veut rehausser les arêtes et les textures sans annuler les zones de l'image où le niveau de gris est constant, on prendra une combinaison linéaire à coefficients positifs de l'image originale et de son accentuation :
a.I + b.(M# o I) = (a + b).I - b.(M o I) (a, b > 0) ,
où M# est le masque d'accentuation et M le masque de lissage. Par exemple, en prenant a = 1, une zone de l'image où le niveau de gris est constant sera préservée. Sur l'arête "marche" on obtient :
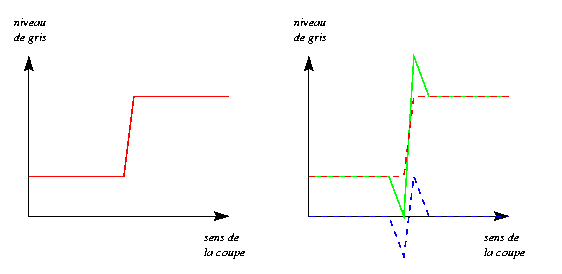
A gauche, le profil de niveaux de gris de la marche dans le sens
perpendiculaire à l'arête (en rouge) ;
A droite, le profil de la marche après ajout de l'accentuation
(en vert), et en pointillés :
le profil original (en rouge) et celui de l'arête
accentuée (en bleu).
Nous illustrons ci-dessous cet effet pour a = b = 1 et le deuxième masque d'accentuation vu plus haut :
 |
 |
|
| Image originale. | Rehaussement par ajout de l'accentuation à l'image. |
On remarquera que les arêtes et textures seront plus
marquées, tandis que les zones à faible variation de
niveaux de gris seront essentiellement préservées.