Une réduction d'une figure signifie toute opération enlevant des pixels de cette figure. Nous considérons le cas où celle-ci doit préserver la topologie de cette figure. Rappelons que la topologie d'une figure est donnée par l'arborescence des composantes connexes de la figure et du fond, et qu'elle dépend donc du choix de l'adjacence sur la figure (avec l'adjacence opposée sur le fond). Nous verrons plus loin que la préservation globale de la topologie entre les deux figures est insuffisante, qu'il faut pouvoir déformer continûment une figure en l'autre, ce qu'on appelle l'homotopie.
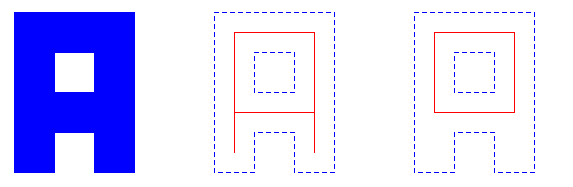
Un exemple bien connu de réduction est la squelettisation, qui réduit la figure à un squelette épais d'un pixel, ayant la même forme générale et la même topologie que la figure. Un autre exemple est la réduction ultime, qui enlève les pixels de la figure jusqu'à ce que ce ne soit plus possible sans modifier la topologie ; elle peut par exemple être obtenue en enlevant l'un après l'autre tous les pixels simples du squelette. Nous illustrons ces deux opérations ci-dessous :

A gauche, la figure de départ ; au milieu sa squelettisation ; à droite, sa réduction ultime.
Soit F0 la figure initiale, de fond B0 = Z2 \ F0. La réduction enlève de F0 une partie K, et donne la figure finale F1, de fond B1 = Z2 \ F1. On a :
| F1 = F0 \ K , | B1 = B0  K
, K
, |
||
F0 = F1  K
, K
, |
B0 = B1 \ K . |
On suppose la figure F0 bornée (donc F1 le sera aussi), on a donc une composante connexe du fond entourant toute la figure, elle correspond à la racine de l'arborescence des composantes connexes de la figure et du fond.
On remarque que les formules liant F0 avec F1, et B0 avec B1, sont symétriques par rapport à la double interversion F1 <-> B0 et F0 <-> B1. Donc on peut dire :
Donc si on fait un négatif dans l'image binaire (et qu'on borne la figure du négatif en l'entourant d'une composante connexe du fond), on aura une réduction de la figure, mais on aura interverti les situations initiale et finale, comme illustré ci-dessous :
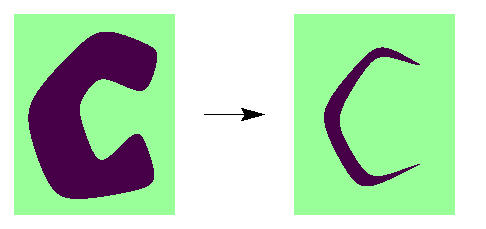
La figure foncée sur fond clair est réduite de gauche à droite.
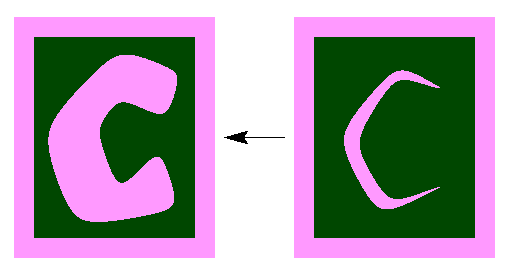
En négatif (inversant la figure et le fond) :
la figure foncée sur fond clair est réduite de droite
à gauche.
L'image en négatif, avec une nouvelle composante du fond entourant le reste, a la même arborescence de composantes connexes, sauf qu'on a rajouté une nouvelle racine à celle-ci (correspondant à la nouvelle composante du fond entourant le reste), et qu'on aura remplacé l'adjacence sur la figure par l'adjacence opposée qu'on avait sur le fond. La préservation de la topologie sera vérifiée dans le négatif comme dans le positif (en choisissant l'adjacence opposée dans le négatif). On en déduit le principe suivant :
Les conditions de préservation de la topologie pour la 8-adjacence sur la figure, correspondent à celles pour la 4-adjacence, à condition d'intervertir les rôles de la figure et du fond, et des situations initiale et finale.
Par exemple, dans le cas où K est un singleton, la topologie est préservée si et seulement si le pixel est simple, et cela se mesure par le nombre de Yokoi correspondant à la connexité choisie sur la figure ; on remarquera que la formule du nombre de Yokoi en 8-connexité est obtenue à partir de celle du nombre de Yokoi en 4-connexité, en y intervertissant les valeurs figure/fond.
Que la figure réduite ait la même topologie que la figure initiale ne suffit pas. Nous allons voir qu'il est nécessaire que la topologie soit préservée tout au long du processus de réduction. Nous illustrons cela dans deux exemples concrets ci-dessous ; à gauche on a la figure initiale, au milieu les pixels à enlever sont hachurés, et à droite on a la figure réduite :
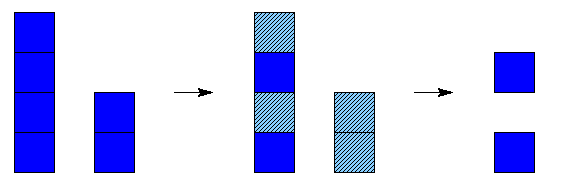
Ici, la figure initiale et la figure réduite ont chacune deux composantes connexes sans trous. La réduction efface une composante connexe de la figure et scinde une autre en deux.
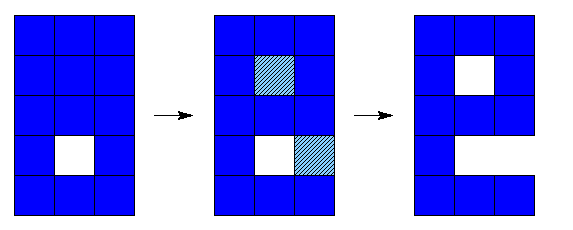
Ici, la figure initiale et la figure réduite ont chacune une composante connexe avec un trou. La réduction crée une composante connexe du fond et en fusionne deux autres.
Dans les deux cas, la réduction applique à l'image deux modifications opposées de la topologie, qui s'annulent l'une l'autre. Outre le caractère artificiel de cette transformation, cela induit une déformation de la figure. On peut donc exiger de la réduction qu'elle satisfasse les exigences suivantes :
Comme la figure finale (réduite) F1 est incluse dans la figure initiale F0, toute composante k-connexe de F1 est incluse dans une unique composante k-connexe de F0 ; on a donc une application incF de l'ensemble des composantes k-connexes de F1 vers celui des composantes k-connexes de F0, associant à toute composante de F1 celle de F0 qui la contient. De même, comme le fond initial B0 est inclus dans le fond final B1, toute composante k'-connexe de B0 est incluse dans une unique composante k'-connexe de B1 ; on a donc une application incB de l'ensemble des composantes k'-connexes de B0 vers celui des composantes k'-connexes de B1, associant à toute composante de B0 celle de B1 qui la contient. Les 4 exigences ci-dessus peuvent donc s'exprimer comme suit en termes des applications incF et incB :
Donc incF et incB doivent être bijectives. Il y a ainsi une bijection entre les composantes connexes de la figure, avant et après réduction, et une entre celles du fond, après et avant réduction, donnée par l'inclusion. On peut montrer que ces deux bijections établissent un isomorphisme entre l'arborescence des composantes connexes de F0 et B0, et celle des composantes connexes de F1 et B1, en d'autres termes :
pour toute composante k-connexe C de F1 et toute composante k'-connexe D de B0,
incF(C) est adjacente à D si et seulement si C est adjacente à incB(D).
En fait, on peut montrer le résultat suivant :
Soit K une partie non-vide de la figure F0 telle que la réduction enlevant K de F0 vérifie la bijectivité des inclusions incF et incB des composantes connexes, avant et après réduction, de la figure et du fond. Alors on peut écrire K = {p1, ..., pn}, de telle sorte que pour chaque i = 1, ..., n, pi est simple dans F0 \ {pj | j < i }.
En d'autres termes, on peut enlever K de la figure en retirant successivement des pixels simples. Comme la topologie est préservée à chaque retrait de pixel simple, la réduction enlevant K préservera la topologie.
Le résultat ci-dessus indique que lorsque les inclusions incF et incB sont bijectives, la figure réduite F1 peut être obtenue à partir de la figure initiale F0 par déformation progressive, en enlevant successivement un pixel simple à la fois. Par ailleurs, si on se place à une résolution plus fine, la topologie de la figure reste la même, et les inclusions incF et incB ne changent pas ; aussi chaque pixel simple à la résolution grossière correspond à un carré de pixels à la résolution fine, qui peut être enlevé par une succession de retraits de pixels simples, comme illustré ci-dessous :
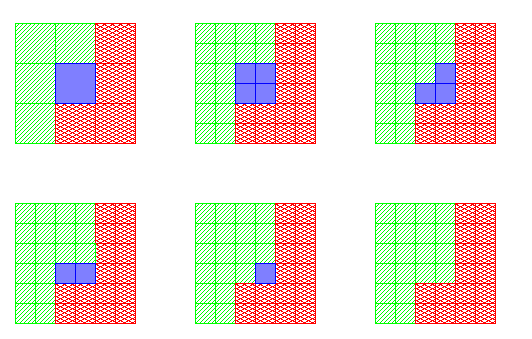
En haut à gauche : un pixel simple (en bleu) entre la
figure (en
rouge avec double hachure) et le fond (en vert avec simple
hachure).
En haut au milieu : la résolution est doublée, le
pixel devient un carré 2 × 2.
Ensuite : ce carré peut être enlevé en
retirant successivement 4 pixels simples.
En topologie, on appelle homotopie la déformation continue d'un objet en un autre. Par conséquent, la réduction d'une figure par succession de retraits de pixels simples est appelée réduction homotopique. En particulier, les algorithmes de squelettisation seront homotopiques, c.-à-d. fondés sur le retrait successif de pixels vérifiant certains critères liés à leur voisinage, dont la simplicité.