Un pixel d'une figure F est dit simple, si la topologie de la figure ne change pas quand on retire ce pixel de la figure ; réciproquement, un pixel du fond B est simple si la topologie de la figure ne change pas quand on ajoute ce pixel à la figure. Ici la topologie s'entend au sens de l'arborescence des composantes connexes de la figure F et du fond B, et dépend donc du choix des adjacences pour la figure et le fond.
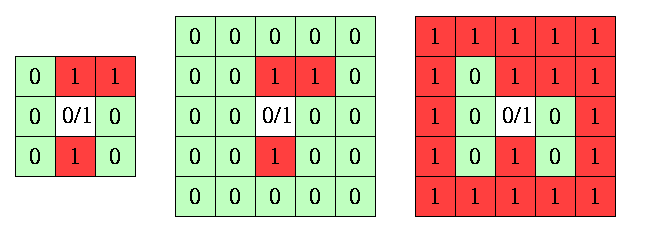
On peut montrer que la simplicité d'un pixel p d'une figure F ne dépend que de la configuration de pixels de la figure et du fond dans V8(p), le 8-voisinage de p formé des 8 pixels 8-adjacents à p. Par conséquent, pour vérifier si p est simple, on peut faire comme si la figure F était incluse dans V8(p), et tous les pixels extérieurs à ce 8-voisinage étaient dans le fond (ou bien, comme si le fond B était inclus dans V8(p)). C'est ce que nous illustrons dans la figure ci-dessous, où les pixels de la figure sont marqués "1" et ceux du fond sont marqués "0".

A gauche, on montre un pixel non-simple p (marqué "0/1"), entouré de son 8-voisinage V8(p). Au milieu, on suppose que la figure est restreinte à V8(p), et alors en retirant le pixel de la figure, une composante connexe de la figure est scindée en deux. A droite, on suppose que le fond est restreint à V8(p), et alors en retirant le pixel de la figure, deux composantes connexes du fond sont fusionnées.
Il est possible de caractériser la simplicité d'un pixel au moyen
du nombre de Yokoi correspondant à la connexité
sur la figure. Il s'agit d'une formule calculée à partir
des valeurs (1 ou 0) des pixels dans le 8-voisinage du pixel
examiné.
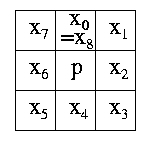
Numérotons les 8 pixels voisins du pixel p de 0 à 7, suivant l'ordre des aiguilles d'une montre, avec 0 pour celui au dessus de p, et soient x0, ..., x7 les valeurs booléennes de leur marquage (1 pour un pixel de la figure, 0 pour un du fond), avec x8 = x0, comme indiqué ci-contre :
Avec la 4-adjacence sur la figure (et la 8-adjacence sur le fond), le nombre de Yokoi de p vaut :
Y4(p) = x0 (1 - x1x2) + x2 (1 - x3x4) + x4 (1 - x5x6) + x6 (1 - x7x8)
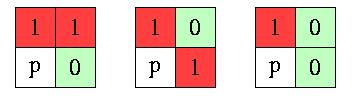
En d'autres termes, on compte le nombre de configurations de coin x2i / x2i+1 / x2i+2 (i = 0, 1, 2, 3) de V8(p), ayant la forme 1/1/0, 1/0/1 ou 1/0/0 :
Avec la 8-adjacence sur la figure (et la 4-adjacence sur le fond), il faut remplacer dans cette formule chaque xi par son complément booléen x'i = 1 - xi, et l'on obtient :
Y8(p) = x'0 (1 - x'1x'2) + x'2 (1 - x'3x'4) + x'4 (1 - x'5x'6) + x'6 (1 - x'7x'8)
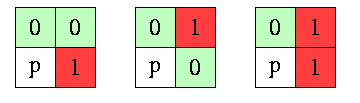
Ici on compte le nombre de configurations de coin x2i / x2i+1 / x2i+2 (i = 0, 1, 2, 3) de V8(p), ayant la forme 0/0/1, 0/1/0 ou 0/1/1 :
Les deux nombres de Yokoi Y4(p) et Y8(p) ont leur valeur comprise entre 0 et 4. On obtient alors la caractérisation suivante de la simplicité d'un pixel :
Un pixel est simple si et seulement si le nombre de Yokoi correspondant à l'adjacence choisie pour la figure vaut 1.