Avec les maillages carré (en deux dimensions) et cubique (en trois dimensions), il est nécessaire de considérer des choix opposés d'adjacence et de connexité pour la figure et le fond : en maillage carré (resp., cubique), si on utilise la 4-connexité (resp., 6-connexité) pour la figure, il faudra prendre la 8-connexité (resp., 26-connexité); pour le fond, et vice versa.
Ce genre de problème ne se pose pas pour le maillage triangulaire correspondant au pavage hexagonal, pour lequel il n'y a qu'une seule relation d'adjacence (la 6-adjacence). C'est une illustration des problèmes mathématiques et algorithmiques liés à la multiplicité des relations d'adjacence.
Nous expliquons ci-dessous le pourquoi de cette dualité figure-fond dans le cas du maillage carré en deux dimensions. Tout cela s'extrapole naturellement au maillage cubique en trois dimensions.
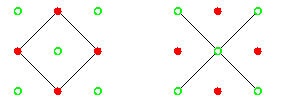
Les choix opposés des connexités pour la figure et le fond sont illustrés ci-dessous, les pixels de la figure étant en rouge et ceux du fond en vert :

Si on considère la 8-connexité sur la figure, alors celle-ci est connexe et forme un anneau entourant un pixel du fond, qui désormais ne peut pas être connecté aux autres pixels du fond ; donc on considère la 4-connexité sur le fond. Par contre, en considérant la 4-connexité sur la figure, celle-ci a alors 4 composantes connexes isolées, et le pixel du fond au milieu de celles-ci est désormais connecté aux autres pixels du fond ; donc on considère la 8-connexité sur le fond.
Le problème se comprend mieux si on reconstruit à partir d'une figure discrète (dans Z2) une figure euclidienne (dans R2), en associant à tout pixel p une cellule C(p) qui est en fait le pavé carré correspondant, contenant son bord. En d'autres termes, C(p) est le carré fermé (contenant son bord) de côté 1 centré en p ; si p est de coordonnées (i,j), C(p) comprendra tous les points de coordonnées (x,y), avec x compris entre i-1/2 et i+1/2, et y compris entre j-1/2 et j+1/2, c.-à-d.
C(p) = [i-1/2,i+1/2] × [j-1/2,j+1/2].
La différence entre la 4- et la 8-adjacence a lieu pour deux pixels diagonalement adjacents, aussi le problème des choix opposés de connexité pour la figure et le fond se pose pour un carré de pixels, comprenant deux pixels de la figure diagonalement adjacents et deux pixels du fond diagonalement adjacents, comme ci-dessous (à nouveau les pixels de la figure sont en rouge et ceux du fond en vert) :
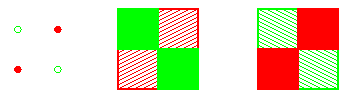
On peut se poser la question de savoir quelle est la couleur du point à l'intersection des 4 cellules carrées. Soit il a la couleur du fond (vert), et ainsi les deux cellules correspondant aux pixels du fond se touchent, tandis que les deux cellules correspondant aux pixels de la figure ne se touchent pas ; cela correspond à la 8-adjacence sur les pixels du fond et la 4-adjacence sur ceux de la figure. Soit il a la couleur de la figure (rouge), et ainsi les deux cellules correspondant aux pixels de la figure se touchent, tandis que les deux cellules correspondant aux pixels du fond ne se touchent pas ; cela correspond à la 8-adjacence sur les pixels de la figure et la 4-adjacence sur ceux du fond.
On peut associer à tout ensemble X de pixels une reconstruction R(X) qui est l'union de toutes les cellules C(p) pour les pixels p de X. C'est un polygone fermé (contenant son bord). Ecrivons R°(X) pour le polygone ouvert correspondant, obtenu en enlevant le bord de R(X). Soit F une figure, et soit B = Z2 \ F le fond correspondant. Alors R(F) et R(B) s'intersectent en leur bord, et on a ainsi
R°(B) = R2 \ R(F) et R°(F) = R2 \ R(B).
Ceci est illustré ci-dessous pour une figure dont nous montrons la restriction à une portion rectangulaire du plan ; les pixels de la figure sont en rouge, ceux du fond en vert, et la ligne bleue représente le bord de la portion de plan.

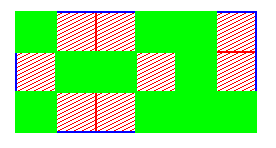
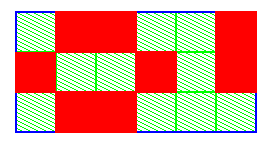
Comme on peut le voir, deux pixels 8-adjacents de F ont leurs cellules se touchant dans R(F), tandis que deux pixels 4-adjacents de F ont leurs cellules se touchant dans R°(F). Plus généralement :
On a la même chose pour B. Or nous avons vu plus haut que le complémentaire dans R2 de R(F) est R°(B) ; cette partition de R2 signifie que dans la reconstruction, les bords entre cellules de la figure et du fond appartiennent toujours à la figure, et correspond au choix de la 8-connexité sur la figure et de la 4-connexité sur le fond. Inversement, le complémentaire dans R2 de R°(F) est R(B)) ; la partition de R2 signifie ici que les bords entre cellules de la figure et du fond appartiennent toujours au fond, et correspond au choix de la 4-connexité sur la figure et de la 8-connexité sur le fond.
Le même raisonnement s'applique pour le maillage cubique en trois dimensions, en prenant les 6- et 26-adjacences à la place des 4- et 8-adjacences.