Etant donnés deux ensembles X et Y de pixels dans Z2, on dira que Y entoure X si tout 4-chemin allant de X vers l'infini doit intersecter Y. Dans le cas où X et Y sont inclus dans une grille rectangulaire G, on exige que tout 4-chemin d'un pixel de X à un pixel du pourtour de la grille G doit intersecter Y.
Nous reprenons l'analyse entamée dans le document précédent. On suppose la figure F bornée, donc incluse dans une grille rectangulaire G telle que tous les pixels sur le pourtour de la grille soient dans le fond B.
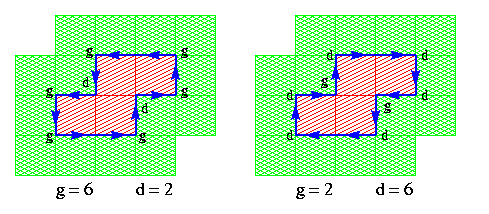
Considérons une composante k-connexe X de F, et une composante k'-connexe Y de B adjacente à X. L'arête entre X et Y forme des cycles pour l'algorithme de suivi. On peut montrer que :

Ceci est illustré ci-dessus, où la composante connexe de la figure (en rouge) est entourée par celle du fond (en vert). On notera que l'orientation opposée de l'arête intervertit les tournants à gauche et à droite.
On construit un graphe dont les sommets sont les composantes k-connexes de F et les composantes k'-connexes de B, et une arête joint deux sommets correspondant à une composante k-connexe de F et une composante k'-connexe de B qui sont adjacentes. On peut alors montrer que :
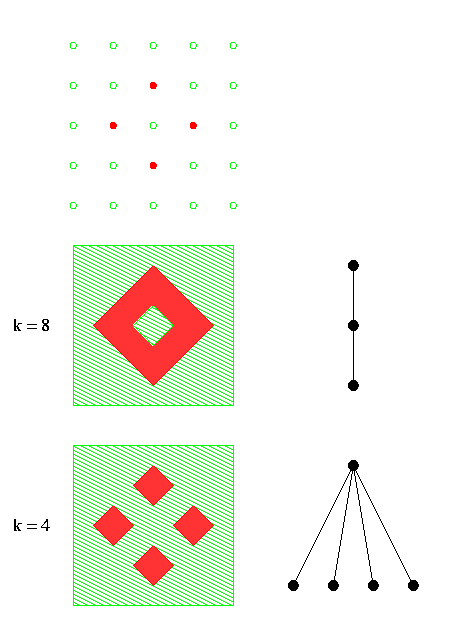
Nous illustrons cette arborescence sur un exemple. En haut nous donnons une image binaire, les pixels de la figure sont en rouge, et ceux du fond en vert. En dessous, nous montrons successivement pour k = 8 et k = 4, à gauche une figure euclidienne ayant la même topologie, et à droite l'arborescence formée par le graphe d'adjacence des composantes connexes.