Les conditions de Montanari sur les coefficients a et b pour un masque de chanfrein 3 × 3 sont très générales, elles sont satisfaites par de nombreuses distances, dont d4 et d8. La question se pose alors d'un choix optimal des coefficients afin d'approximer la distance euclidienne. Ce problème a été étudié en détail par Borgefors, qui a donné deux critères :
Soit d la distance de chanfrein. Bien qu'étant utilisée sur le plan discret Z2, on peut considérer qu'elle est définie sur le plan euclidien R2 (comme pour d4 et d8, il suffit d'étendre les formules de Z2 à R2). Etant donnés deux points p et q de R2, l'erreur |d(p,q) - de(p,q)| sur leur distance croît quand q s'éloigne de p. On considèrera donc l'erreur relative |d(p,q) - de(p,q)| / de(p,q). Pour simplifier les calculs, Borgefors considère la valeur suivante pour l'erreur relative sur p,q de la distance d par rapport à de :
er(d,p,q) = |d(p,q) - de(p,q)| / d8(p,q).
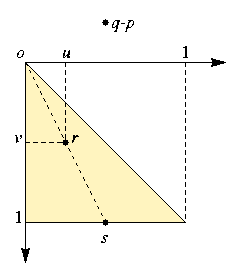
L'erreur relative est invariante par translations, c.-à-d. pour tout vecteur x on a er(d,p,q) = er(d,p+x,q+x). Elle est également invariante par homothéties, c.-à-d. pour tout scalaire r > 0 on a er(d,p,q) = er(d,rp,rq). Enfin, comme le masque de chanfrein est symétrique, l'erreur relative est invariante par rotations de quarts de tour et par symétries axiales ou diagonales. Soit o = (0,0) l'origine du plan, soient u et v les valeurs absolues des coordonnées de q-p (v étant la plus grande des deux), et soient r = (v,u) et s = (1,u/v). On a alors :
er(d,p,q) = er(d,o,q-p) = er(d,o,r) = er(d,o,s) .
L'erreur relative maximale de d par rapport à de est le maximum ermax(d) des erreurs relatives er(d,p,q) pour p et q dans le plan R2. On a ainsi :
ermax(d)= max {er(d,o,x) | x = (1,w), w entre 0 et 1}.
Le premier critère de Borgefors est qu'il faut choisir d de telle sorte que l'erreur relative maximale ermax(d) soit la plus petite possible. A première vue on pourrait penser que le bon choix de la distance d'un point à ses voisins serait a = 1 pour les voisins axiaux et b = sqrt(2) pour les voisins diagonaux. Si cette distance correspond exactement à la distance euclidienne dans les directions axiales et diagonales, par contre dans les directions intermédiaires la distance sera surévaluée par rapport à la distance euclidienne, parce que le chemin de poids minimum empruntera un tronçon axial et un tronçon diagonal, et sera donc plus long qu'un chemin rectiligne euclidien. Afin de réduire l'erreur relative maximale, il faut légèrement diminuer ces valeurs. Les calculs de Borgefors montrent que l'erreur relative maximale est minimisée pour
a = 0,95509... et b = 1,336930..., avec ermax(d)= 0,04491...
tandis qu'en fixant a = 1, le minimum d'erreur relative maximale est obtenu pour
b = 1,35070..., avec ermax(d)= 0,06351...
Une bonne approximation de ces valeurs par des fractions est donnée par a = 1 et b = 4/3, avec ermax(d)= 0,0809... (environ 8%). Cette distance est la moyenne pondérée (1/3) d4 + (2/3) d8. Comme expliqué dans le document précédent, il est plus simple pour les calculs de multiplier cette distance par 3, donc de considérer la distance d4 + 2 d8 donnée par le masque de chanfrein ayant les coefficients a = 3 et b = 4, en sachant que cette distance est une approximation de 3 de. On écrira cette distance d3,4, et on l'appellera la distance (3,4) de Borgefors.
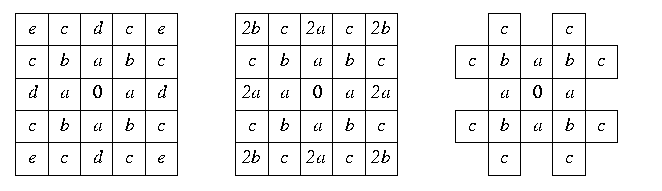
On peut étendre le voisinage d'un pixel à un carré 5 × 5 centré en celui-ci. Un masque de chanfrein 5 × 5, compte tenu de la symétrie de la distance, ne comprend que 5 coefficients. Il est nécessaire que les coefficients d et e correspondant aux voisins distants de 2 selon les axes et les diagonales, soient égaux à 2a et 2b respectivement. Ces coefficients sont alors redondants dans le calcul des distances, et il ne reste ainsi que 3 coefficients a, b et c.
Borgefors a donné les conditions de Montanari pour un masque 5 × 5 :
0 < 2a
c
Notons que 2a c
a + b implique
a b, tandis que
c a + b
et 3b 2c
impliquent b
2a : on retrouve ainsi les conditions de Montanari d'un
masque 3 × 3 (à savoir 0 < a b 2a) comme conséquences de celles
5× 5.
Ces conditions sur le masque 5 × 5 se justifient en termes de chemins les plus courts, de manière semblable à ce que nous avons expliqué précédemment pour le masque 3 × 3. Si a = 0, la distance d'un pixel à ses 4-voisins est nulle. Si c < 2a, alors le chemin le plus court d'un pixel à un autre situé à 4 unités de celui-ci selon un axe, sera formé de deux déplacements "du cavalier" (de 2 selon un axe et 1 selon l'autre axe), et la distance entre ces deux pixels sera donc de 2c au lieu de 4a. Si a + b < c, alors le chemin le plus court d'un pixel à un autre situé à 2 unités de celui-ci selon un axe et 1 selon l'autre, sera formé d'un déplacement axial et d'un diagonal, et la distance entre ces deux pixels sera donc de a + b au lieu de c. Si 2c < 3b, alors le chemin le plus court d'un pixel à un autre situé à 3 unités de celui-ci selon une diagonale, sera formé de deux déplacements "du cavalier", et la distance entre ces deux pixels sera donc de 2c au lieu de 3b.
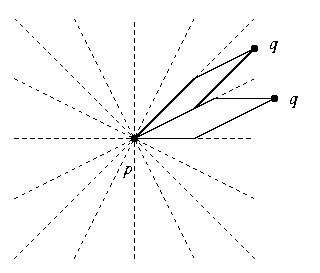
Le masque 5 × 5 détermine dans le plan 16 directions (données par les vecteurs (±1,0), (0,±1), (±1,±2) et (±2,±1) correspondant aux cases du masque). Lorsque les conditions de Montanari sont satisfaites, étant donnés deux pixels p et q, tout chemin de poids minimum de p à q empruntera, parmi ces 16 directions, uniquement les deux directions les plus proches de celle du vecteur pq (en particulier, uniquement la direction de pq quand celui-ci est selon une de ces 16 directions).
Les calculs de Borgefors montrent qu'en fixant a = 1, le minimum d'erreur relative maximale est obtenu pour
c = 2,19691... et b compris entre 1,39463... et 1,43155..., avec ermax(d)= 0,01958...
Une bonne approximation de ces valeurs par des fractions est donnée par a = 1, b = 7/5 et c = 11/5, avec ermax(d)= 0,0202 (environ 2%). Notons qu'ici 7/5 et 11/5 sont des approximations de sqrt(2) et sqrt(5), qui sont les distances euclidiennes des points correspondants du masque à l'origine. Comme plus haut, il est plus simple de multiplier cette distance par 5, donc de considérer la distance donnée par le masque de chanfrein ayant les coefficients a = 5, b = 7 et c = 11, en sachant que cette distance est une approximation de 5 de. On écrira cette distance d5,7,11, et on l'appellera la distance (5,7,11) de Borgefors.