Nous avons vu dans le document précédent que la 4-distance sur-évalue la distance euclidienne, tandis que la 8-distance la sous-évalue.
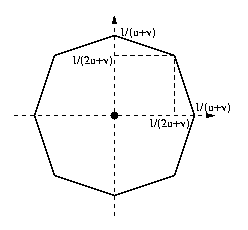
Pour corriger ce défaut, une possibilité serait de prendre une moyenne pondérée des 4- et 8-distances, donc une distance d de la forme r d4 + s d8, où r et s sont non-négatifs et r + s = 1. Généralement r et s sont rationnels, et on peut écrire r = u/w et s = v/w ; pour éviter de traîner le dénominateur w dans les calculs de distances, on multipliera la distance par w et on considèrera ainsi la distance u d4 + v d8, u et v étant des entiers non-négatifs tels que u + v > 0, en retenant que la distance ainsi estimée est une approximation de w de. Le fait que u et v soient non-négatifs et de somme strictement positive garantit que la distance ainsi obtenue vérifie les axiomes vus plus haut. Ici la distance d'un pixel à ses voisins axiaux sera u + v, tandis que sa distance à ses voisins diagonaux sera 2u + v. Le cercle unité pour cette distance sera un octogone dont les sommets sont de coordonnées (±1/(u+v),0), (0,±1/(u+v)) et (±1/(2u+v),±1/(2u+v)).
Dans le cas de la 4-distance, on a u = 1 et v = 0, et on retrouve le losange inscrit dans le cercle unité, tandis que pour la 8-distance, on u = 0 et v = 1, et on retrouve le carré circonscrit autour du cercle unité.
Une autre approche consiste à mettre une pondération sur l'adjacence d'un pixel à ses voisins, valant la distance entre ces deux pixels. On donne ainsi à Z2 la structure d'un graphe pondéré, dont les arêtes sont celles de la 8-adjacence, et où l'arête entre deux pixels voisins p et q a un poids P(p,q). Etant donné un 8-chemin p = x0, ..., xn = q du pixel p au pixel q, le poids de ce chemin est la somme des poids des arêtes dans celui-ci, à savoir
P(x0,x1) + ... + P(xn-1,xn).
Dans ce graphe pondéré, la distance d(p,q) entre le pixel p et le pixel q est le poids minimum d'un 8-chemin de p à q. Cette distance vérifie bien les trois axiomes donnés plus haut.
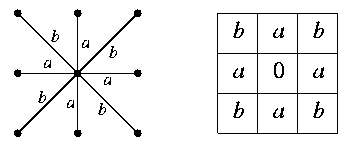
On donnera une pondération a à l'adjacence selon un axe, et b à l'adjacence selon une diagonale, où a,b > 0. Ce choix de pondération des arêtes de la 8-adjacence (cfr. ci-dessous à gauche) peut être représenté par un tableau 3 × 3 donnant les distances d'un pixel à chacun de ses 8 voisins (a et b), ainsi que celle à lui-même (0), comme illustré ci-dessous à droite :

Ce tableau est appelé masque de chanfrein, et la distance correspondante distance de chanfrein. On a la 8-distance pour a = b = 1, et la 4-distance pour a = 1 et b = 2. On retrouve également la combinaison pondérée u d4 + v d8 des 4- et 8-distances en prenant a = u + v et b = 2u + v. Le mot chanfrein utilisé pour désigner une telle distance vient du fait que pour celle-ci le cercle unité forme un octogone (cfr. plus haut), de sommets (±1/a,0), (0,±1/a) et (±1/b,±1/b).
Montanari a donné les conditions que doivent satisfaire les coefficients a et b d'un masque de chanfrein 3 × 3, à savoir :
0 < a
b
2a (ce qui implique en particulier que b > 0).
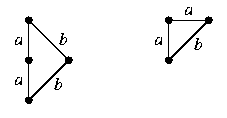
La nécessité de telles conditions se fait clairement sentir. Si a = 0, la distance d'un pixel à ses 4-voisins est nulle, ce qui contredit l'axiome de positivité. Si b < a, alors le chemin le plus court d'un pixel à un autre situé à 2 unités de celui-ci selon un axe, sera formé de deux déplacements diagonaux, et la distance entre ces deux pixels sera donc de 2b au lieu de 2a. Si b > 2a, alors le chemin le plus court d'un pixel à un autre voisin diagonalement de celui-ci, sera formé de deux déplacements horizontal et vertical, et la distance entre ces deux pixels sera donc de 2a au lieu de b.
Notons également que les conditions de Montanari sont nécessaires et suffisantes pour que l'octogone de sommets (±1/a,0), (0,±1/a) et (±1/b,±1/b), soit convexe. Il représente alors le cercle unité pour la distance de chanfrein.
Nous avons vu plus haut que la combinaison pondérée u d4 + v d8 des 4- et 8-distances est la distance de chanfrein correspondant à a = u + v et b = 2u + v. On obtient ainsi u = b - a et v = 2a - b, donc les conditions de Montanari sont équivalentes au fait que les coefficients u et v soient non-négatifs et de somme strictement positive, condition pour qu'une telle combinaison de d4 et d8 soit une distance.
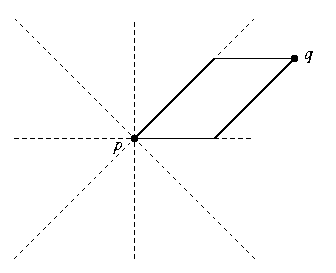
Quand les conditions de Montanari sont satisfaites, étant donnés deux pixels p et q, tout chemin de poids minimum de p à q empruntera, parmi les 8 directions axiales et diagonales, uniquement les deux directions les plus proches de celle du vecteur pq (en particulier, uniquement la direction de pq quand celui-ci est selon une de ces 8 directions). Par exemple, si q est situé, par rapport à p, h unités à droite et v unités en haut, avec v < h, alors un chemin de poids minimum de p à q comportera nécessairement h - v déplacements horizontaux d'une unité à droite et v déplacements diagonaux d'une unité en haut et à droite :