V8(p) qui sont 4-adjacentes à
p ;
V8(p) (elles sont nécessairement
8-adjacentes à p).
Nous allons décrire en détail les changements possibles de topologie d'une figure induits par le retrait d'un pixel de cette figure. Nous verrons que ceux-ci dépendent essentiellement de la configuration de pixels de la figure et du fond dans le 8-voisinage de ce pixel.
Etant donné un pixel p, nous écrivons V4(p) et V8(p) pour le 4- et le 8-voisinage de p, formés respectivement des pixels 4- ou 8-adjacents à p. Pour un ensemble X de pixels, soient
V8(p) qui sont 4-adjacentes à
p ;
V8(p) (elles sont nécessairement
8-adjacentes à p).
On peut vérifier que ces deux entiers sont compris entre 0 et 4.
On suppose une figure F0 bornée, de fond
B0. Soit p un pixel de
F0, posons F1 = F0 \
{p} et B1 = B0 
{p}, la figure et le fond
obtenus en retirant p de F0. Soient
k et k' les choix d'adjacences sur la figure et le
fond (donc {k,k'} = {4,8}). On
considère :
V8(p) qui sont k-adjacentes
à p ;
V8(p) qui sont k'-adjacentes
à p.
La configuration de pixels de F1 et de B0 dans V8(p) détermine les types de changements de topologie de la figure F obtenus quand on retire p de F0. Nous avons 3 cas :
Donc F1
Vk(p) = Ø et
Ck(p,F1) =
0. En d'autres termes, p est isolé dans
F0, et {p} est une composante
k-connexe de F0. Nous illustrons
ci-dessous la configuration de pixels de F1
(marqués "1") et de B0
(marqués "0") dans
V8(p), selon que k = 4 ou
k = 8 ; ici le symbole "*" signifie
"indifféremment 1 ou 0" :
|
|
|||||||||||||||||||
| k = 4 | k = 8 |
On voit que tant pour k = 4 que pour k = 8, {p} est une composante k-connexe de F0 entourée par une composante k'-connexe de B0, en fait Ck'(p,B0) = 1. Donc quand on enlève p de F0, la composante k-connexe {p} de F0 est effacée, et la composante k'-connexe de B0 entourant p est agrandie.
Par conséquent, en enlevant p de la figure, le nombre de composantes k-connexes de la figure diminue de 1, tandis que le nombre de composantes k'-connexes du fond ne change pas, et ainsi le nombre d'Euler diminue de 1.
Donc B0
Vk'(p) = Ø et
Ck'(p,B0) =
0. En d'autres termes, p est isolé dans
B1, et {p} est une composante
k'-connexe de B1. Nous illustrons
ci-dessous la configuration de pixels de F1 et de
B0 (ou indifféremment dans
F1 ou B0, marqués
"*") dans V8(p), selon que
k = 4 ou k = 8; :
|
|
|||||||||||||||||||
| k = 4 | k = 8 |
On voit que tant pour k = 4 que pour k = 8, {p} est une composante k'-connexe de B1 entourée par une composante k-connexe de F1, en fait Ck(p,F1) = 1. Donc quand on enlève p de F0, la composante k-connexe de F0 contenant p est diminuée, et une nouvelle composante k'-connexe {p} de B1 est créée.
Par conséquent, en enlevant p de la figure, le nombre de composantes k-connexes de la figure ne change pas, tandis que le nombre de composantes k'-connexes du fond augmente de 1, et ainsi le nombre d'Euler diminue de 1.
Donc F1
Vk(p) et B0
Vk'(p) sont non-vides. Soient
r le nombre de composantes k-connexes de
F1 k-adjacentes à p, et
s le nombre de composantes k'-connexes de
B0 k'-adjacentes à p,
donc r, s > 0. Quand on enlève p
de F0, la composante k-connexe de
F0 contenant p est scindée en
r composantes k-connexes de F1
(il n'y a pas scission pour r = 1), tandis que s
composantes k'-connexes de B0 sont
fusionnées en une composante k'-connexe de
B1 (il n'y a pas fusion pour s = 1). Par
conséquent, en enlevant p de la figure, le nombre de
composantes k-connexes de la figure augmente de r -
1, tandis que le nombre de composantes k'-connexes du fond
diminue de s - 1, et ainsi le nombre d'Euler augmente de
r +s - 2.
Quand on enlève p de G0 =
(F1 V8(p)) {p}, la composante
k-connexe contenant {p} est scindée en
Ck(p,F1)
composantes k-connexes de F1 V8(p),
tandis que le fond reste k'-connexe ; ainsi le nombre
d'Euler de G0 augmente de
Ck(p,F1)
-1. Prenons la figure H0 formée de
G0 et d'une bande entourant
V8(p) ; en enlevant p de
H0, la figure reste k-connexe, tandis que
les
Ck'(p,B0)
composantes k'-connexes du fond k'-adjacentes
à p sont fusionnées ; ainsi le nombre
d'Euler de H0 augmente de
Ck'(p,B0) -
1.
Mais nous avons vu dans l'étude du
nombre d'Euler que celui-ci peut être calculé par
comptage de diverses configurations 2 × 2 de pixels de la figure
et du fond. Par conséquent, quand on enlève un pixel de
la figure, la modification du nombre d'Euler ne dépend que
l'ensemble des configurations 2 × 2 contenant ce pixel, donc du
8-voisinage de celui-ci. Comme les trois figures
F0, G0 et
H0 comprennent les mêmes pixels dans
V8(p), à savoir
F1
V8(p), dans les trois cas le nombre
d'Euler augmente du même montant : r
+s - 2 =
Ck(p,F1) -1
= Ck'(p,B0)
- 1. Ce nombre est compris entre 0 et 3 (parce que
Ck(p,F1)
4). Nous illustrons ci-dessous ce
raisonnement pour k = 4 et
Ck(p,F1) =3.
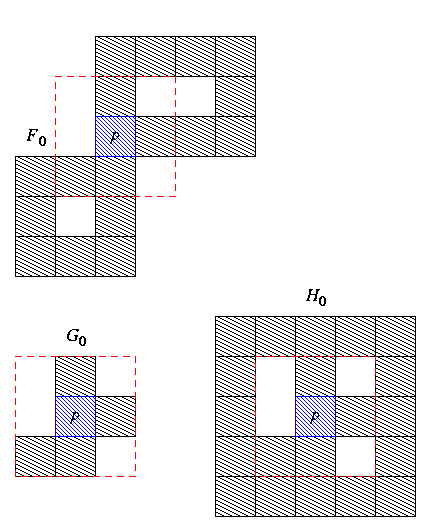
Ici C4(p,F1) =
C8(p,B0) = 3. Le
trait pointillé rouge délimite
V8(p).
En haut : en enlevant p de F0, une
composante 4-connexe de la figure est scindée en 2,
et 2 composantes 8-connexes du fond sont fusionnées.
En bas à gauche : en enlevant p de
G0, une composante 4-connexe de la figure est
scindée en 3.
En bas à droite : en enlevant p de
H0, 3 composantes 8-connexes du fond sont
fusionnées.
En définitive, le nombre de composantes k-connexes de
la figure et de composantes k'-connexes du fond ne changent
pas, si et seulement si
Ck(p,F1) =
Ck'(p,B0) =
1. Dans ce cas, les composantes k-connexes de la figure ne
sont ni effacées ni scindées, tandis que les composantes
k'-connexes du fond ne sont ni créées ni
fusionnées. Ici p est k-adjacent à une
unique composante k-connexe C de
F1, et k'-adjacent à une unique
composante k'-connexe D de
B0 ; la composante k-connexe
C {p} de
F0 est adjacente à la composante
k'-connexe D de B0, et en
enlevant p de la figure, la composante k-connexe
C de F1 est adjacente à la
composante k'-connexe D
{p} de B1. Donc les composantes connexes
de la figure et du fond correspondent, et l'adjacence entre elles est
préservée.
Dans le cas (3°) ci-dessus, on peut montrer
l'égalité
Ck(p,F1) =
Ck'(p,B0)
en remarquant qu'en faisant le tour de
V8(p), les composantes
k-connexes de F1 V8(p)
k-adjacentes à p alternent avec les
composantes k'-connexes de B0 V8(p)
k'-adjacentes à p. En fait, le nombre de Yokoi
Yk(p) compte le nombre de
transitions dans V8(p) entre les
composantes k-connexes de F1 V8(p)
k-adjacentes à p et les composantes
k'-connexes de B0 V8(p)
k'-adjacentes à p. Donc dans les cas (1°)
(Ck(p,F1) =
0, pas de composante k-connexe de F1 V8(p)
k-adjacente à p) et (2°)
(Ck'(p,B0) =
0, pas de composante k'-connexe de B0
V8(p) k'-adjacente à
p), il n'y a aucune transition, et le nombre de Yokoi vaut
0, tandis que dans le cas (3°)
(Ck(p,F1) =
Ck'(p,B0)
> 0), il y a autant de transitions que de composantes de chaque
type, donc le nombre de Yokoi vaut
Ck(p,F1) =
Ck'(p,B0).
Le tableau suivant récapitule les différents cas (ici "C.C." est une abréviation de "composantes connexes de", et "var. Ek" désigne la variation du nombre d'Euler) :
| F1
Vk(p) |
B0
Vk'(p) |
Ck(p,F1) | Ck'(p,B0) | Yk(p) | C.C. figure | C.C. fond | var. Ek |
|---|---|---|---|---|---|---|---|
| vide | non-vide | 0 | 1 | 0 | 1 effacée | préservées | - 1 |
| non-vide | vide | 1 | 0 | 0 | préservées | 1 créée | - 1 |
| non-vide | non-vide | 1 | 1 | 1 | préservées | préservées | 0 |
| t | t | t | 1 scindée en r | s fusionnées | + t - 1 | ||
| t = 2, 3, 4 | r > 0, s > 0, r + s = t + 1 | ||||||
De la discussion précédente, il ressort que la topologie est préservée dans le cas où Ck(p,F1) = Ck'(p,B0) = 1, c.-à-d. si et seulement si le nombre de Yokoi vaut 1.