Le Nombre d'Euler est un entier associé à toute surface orientable. C'est un invariant topologique de celle-ci, dans le sens qu'il ne change pas si la surface subit une déformation continue. Il est obtenu comme suit : on trace un graphe planaire connexe sur la surface, ayant S sommets, A arêtes, et F faces ; le nombre d'Euler est alors l'entier
E = S - A + F.
Ce nombre ne dépend pas du choix du graphe planaire. Dans le cas où la surface est une figure incluse dans le plan euclidien R2, ce nombre est égal au nombre de composantes connexes de la figure moins le nombre de trous. Nous illustrons ci-dessous les deux définitions du nombre d'Euler d'une figure euclidienne (en rouge, le fond étant en vert, et les arêtes du graphe planaire en bleu).

S = 15, A = 21, F = 7, donc E = 15
- 21 + 7 = 1.
Il y a 2 composantes connexes et 1 trou, donc E = 2 - 1 = 1.
Si cette figure est bornée, toutes les composantes connexes du fond sont des trous de la figure, à l'exception de celle entourant toute la figure ; donc le nombre d'Euler sera égal au nombre de composantes connexes de la figure, moins le nombre de composantes connexes du fond, plus un.
Pour les figures dans le plan discret Z2, la définition du nombre d'Euler est celle basée sur le nombre de composantes connexes de la figure et du fond.
Comme vu dans un document précédent, on suppose la figure F bornée, donc incluse dans une grille rectangulaire G telle que tous les pixels sur le pourtour de la grille soient dans le fond B, et on note par k et k' les nombres désignant les adjacences opposées choisies sur F et B respectivement (k = 4 ou 8, et k' = 12 - k, c.-à-d. {k,k'} = {4,8}). On a donc un nombre d'Euler dépendant de k, à savoir
Ek = Ck(F) - Ck'(B) + 1,
où Ck(F) est le nombre de composantes k-connexes de F, et Ck'(B) est nombre de composantes k'-connexes de B.
L'intérêt pratique du nombre d'Euler est qu'il est facile à calculer, il suffit de compter le nombre d'occurrences dans l'image de certaines configurations de pixels de la figure et du fond. Le tableau ci-dessous donne certaines configurations isotropes (définies à une rotation près) de pixels de la figure (marqués 1) et du fond (marqués 0), ainsi que leur nombre.
| Configuration | Description | Nombre | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | pixel de la figure | s | |||||||||||||||||||||||||
|
paire de pixels 4-adjacents de la figure | a | |||||||||||||||||||||||||
|
paire de pixels diagonalement adjacents de la figure | d | |||||||||||||||||||||||||
|
triangle de pixels 8-adjacents de la figure | t | |||||||||||||||||||||||||
|
carré de pixels 8-adjacents de la figure | q | |||||||||||||||||||||||||
|
croisement de paires de pixels diagonalement adjacents de la figure et du fond |
X | |||||||||||||||||||||||||
|
carré avec 3 pixels de la figure et 1 du fond | Q3 | |||||||||||||||||||||||||
|
carré avec 3 pixels du fond et 1 de la figure | Q1 | |||||||||||||||||||||||||
Alors le nombre d'Euler Ek pour la k-adjacence sur la figure (et k'-adjacence sur le fond) s'exprime de deux manières pour k = 4 et 8 :
| E4 = (Q1 - Q3 + 2X) / 4 | E4 = s - a + q | |
| E8 = (Q1 - Q3 - 2X) / 4 | E8 = s - a - d + t -q |
On peut expliquer ces formules. Commençons par celles de gauche pour E4 et E8. Si on fait un suivi d'arête entre la figure et le fond avec l'orientation d'arêtes laissant la figure à gauche, les configurations de type Q1 et Q3 correspondent à un tournant à gauche et à droite respectivement. Par contre une configuration de type X correspond à 2 tournants à gauche ou à droite suivant que k = 4 ou 8 ; il y a 2 tournants parce qu'il faut considérer les éléments d'arête le long des deux pixels de la figure et des deux du fond, comme illustré ci-dessous :
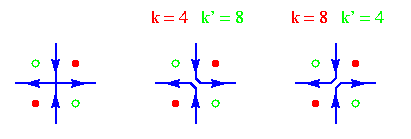
Donc ces formules de gauche comptent le quart de la différence entre le nombre de tournants à gauche et le nombre de tournants à droite dans un suivi d'arête laissant la figure à gauche. Chaque cycle d'arête correspond à l'arête entourant une composante connexe de la figure ou un trou, suivant que la différence entre le nombre de tournants à gauche et le nombre de tournants à droite le long de ce cycle vaut +4 ou -4. Donc le quart de la différence globale donne +1 fois le nombre de composantes connexes et -1 fois le nombre de trous.
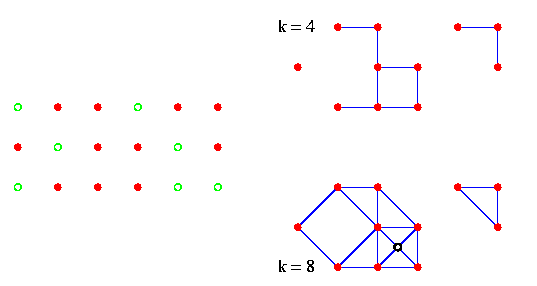
Il est possible de déduire les formules de droite de celles de gauche. On peut cependant les expliquer en termes de sommets, arêtes et faces d'un graphe planaire dessiné sur la figure discrète, comme illustré ci-dessus. Pour k = 4, on prend chaque pixel comme sommet, une arête joint deux pixels 4-adjacents, et une face est un carré formé par 4 pixels mutuellement 8-adjacents dans la figure ; donc il y a s sommets, a arêtes et q faces. Pour k = 8, un pixel est un sommet, une arête joint 2 pixels 8-adjacents, et un triangle de pixels mutuellement 8-adjacents constitue une face ; cependant dans un carré de pixels de la figure, il y aura un sommet supplémentaire au point central du carré, les deux arêtes diagonales seront dédoublées, et les 4 triangles seront ceux joignant 2 sommets consécutifs du carré au point central de celui-ci. Cela donne alors s + q sommets, a + d + 2q arêtes, et t faces.
Il y a également des formules de comptage de configurations non isotropes (définies pour une orientation précise). Nous donnons ci-dessous quatre cas particuliers des configurations Q1, Q3 et X, selon une orientation spécifique :
| Configuration |
|
|
|
|
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nombre | Q1* | Q3* | X+ | X- |
On a alors les formules suivantes, à comparer avec celles vues plus haut utilisant Q1, Q3 et X :
E4 = Q1* - Q3* + X+
E8 = Q1* - Q3* - X-
Expliquons ces formules. Si on fait un suivi d'arête entre la figure et le fond avec l'orientation d'arêtes laissant la figure à gauche, les termes positifs correspondent au nombre de tournants à gauche où l'orientation de l'arête passe d'ouest à sud, tandis que les termes négatifs correspondent au nombre de tournants à droite où l'orientation de l'arête passe de sud à ouest, comme illustré ci-dessous :
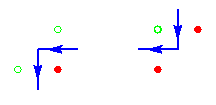
Donc ces formules comptent la différence entre le nombre de changements d'orientation d'ouest à sud et de sud à ouest. Le long d'un cycle de l'arête, cette différence vaut +1 ou -1 selon que ce cycle entoure une composante de la figure ou un trou.
Le nombre d'Euler peut donc être obtenu en comptant le nombre de certaines configurations de pixels de la figure et du fond. Cela peut être réalisé en balayant l'image avec une fenêtre 2 × 2, et en incrémentant le compteur associé aux diverses configurations chaque fois que celles-ci sont rencontrées.
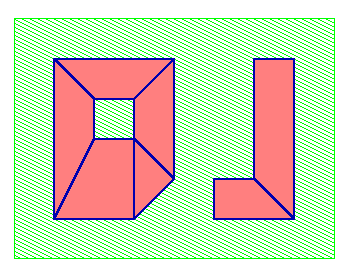
Bien que le nombre d'Euler, c.-à-d. la différence entre le nombre de composantes connexes de la figure et le nombre de trous dans celles-ci, soit calculable par comptage de configurations locales, il n'en est pas de même pour les deux termes de cette différence, à savoir le nombre de composantes connexes de la figure, et le nombre de trous. Cela peut facilement se voir en comparant les deux figures suivantes (en couverture du livre de Minski et Papert sur le "perceptron", un modèle de réseau neuromorphique en IA) :
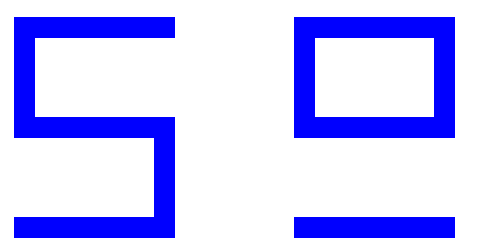
Ces deux figures comportent exactement les mêmes éléments, à savoir deux bandes verticales, deux bandes horizontales, deux extrémités (droite et gauche) de bandes horizontales,et quatre jonctions en coin entre bandes horizontale et verticale (un coin de chaque type). D'ailleurs les deux figures ont la même moitié gauche, tandis que leurs moitiés droites sont composées des mêmes morceaux, mais arrangés dans un ordre différent. Toutes deux ont leur nombre d'Euler égal à 1, mais l'une a une composante connexe sans trou, et l'autre deux composantes connexes et un trou.
Si on connaît le nombre de composantes connexes de la figure, alors le nombre d'Euler permet de donner automatiquement le nombre de trous, et vice versa. Par exemple si on sait que les composantes connexes de la figure sont convexes, alors il n'y a pas de trous, donc le nombre d'Euler sera égal au nombre de composantes connexes de la figure.