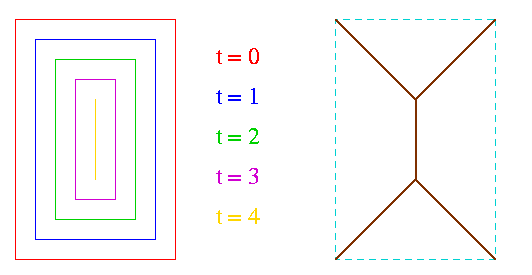
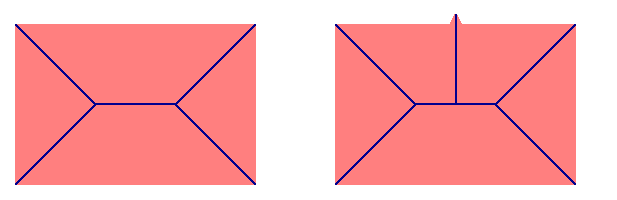
A gauche, les fronts de flamme aux instants t = 0, 1, 2, 3 et 4. A droite, les points de rencontre des fronts de flamme à tous les instants forment le squelette (en brun).
Un squelette d'une figure est une représentation simplifiée de celle-ci,
La première approche envisagée pour définir un squelette se place dans le cadre de la géométrie euclidienne, et est basée sur la transformée de distance euclidienne.
En 1962, Blum propose l'analogie suivante. Supposons que la figure soit une prairie constituée d'herbe sèche, et qu'on y mette le feu simultanément sur tous les points du bord. Le feu se propagera à vitesse constante à l'intérieur de la figure, formant des fronts de flamme. Les points de rencontre des différents fronts de flamme aux divers instants de leur propagation, formeront le squelette. Nous illustrons cela sur une figure en forme de rectangle :
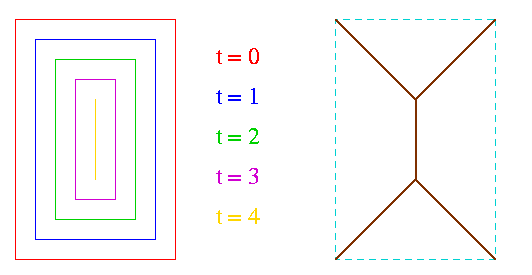
A gauche, les fronts de flamme aux instants t = 0, 1, 2, 3 et
4. A droite, les points de rencontre des fronts de flamme à
tous les instants forment le squelette (en brun).
On peut formaliser cette analogie comme suit. On suppose la vitesse de propagation des flammes égale à un (cela revient à changer l'échelle du temps). Ainsi les points à l'intérieur de la figure appartenant à un front de flamme au temps t sont tous ceux dont la distance au bord est égale à t. Un tel point p est à distance t d'un point q du bord de la figure, qui est à l'origine de la flamme qui a atteint p. La rencontre de deux fronts de flamme a lieu lorsque les flammes issues de deux points distincts q1 et q2 du bord se rencontrent au temps t en un point p (qui est donc à distance t de q1 et de q2).
Soit F la figure et ðF son bord. Soit d la distance euclidienne. On suppose la figure F bornée, et topologiquement fermée, c.-à-d. contenant son bord. Pour un point p de F, soit f(p) = d(p,ðF) la distance de p au bord ðF. Notons que f est la transformée de distance de marqueur ðF dans le masque F. Pour tout point p de F, il existe un point q du bord ðF tel que d(p,q) = f(p). Le point p appartiendra au squelette s'il existe au moins deux points q1 et q2 de ðF, tels que d(p,q1) = d(p,q2) = f(p). Ceci nous donne la :
1ère définition : Le squelette de distance d'une figure F est formé de tous les points p à l'intérieur de F dont la distance au bord ðF de F est atteinte en au moins deux points q1 et q2 de ðF : d(p,q1) = d(p,q2) = d(p,ðF).
Pour un point p et un rayon r positif, la boule Br(p) centrée en p et de rayon r est formée de tous les points q dont la distance d(p,q) à p est inférieure ou égale à r.
Pour un point p de la figure, à distance f(p) = d(p,ðF) du bord, la boule Bf(p)(p) (centrée en p et de rayon f(p)) est incluse dans la figure F. Si p appartient au squelette, on a f(p) = d(p,q1) = d(p,q2) pour deux points q1 et q2 de ðF. Pour une boule Br'(p') centrée en un point p' de F et de rayon r'>r, il est clair que si Br'(p') contient Bf(p)(p), alors q1 ou q2 est à l'intérieur de Br'(p'), ce qui signifie que Br'(p') dépasse du bord de F, comme illustré dans les deux figures ci-dessous :
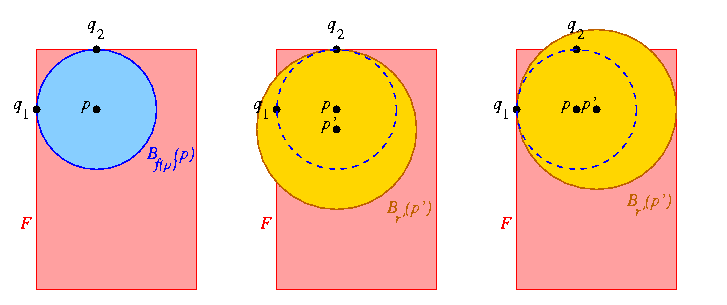
A gauche, F et
Bf(p)(p). Au centre,
q1 est à l'intérieur de
Br'(p'). A droite,
q2 est à l'intérieur de
Br'(p'). Dans ces deux cas,
Br'(p'), dépasse du bord
de F.
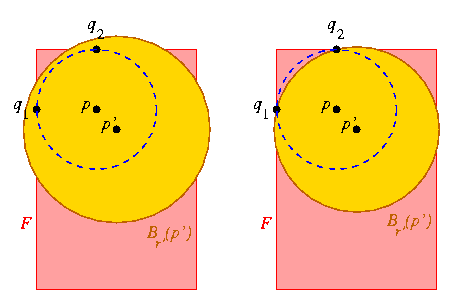
A gauche, q1 et q2 sont
à l'intérieur de
Br'(p'), qui dépasse du
bord de F. A droite, ni q1 ni
q2 n'est à l'intérieur de
Br'(p'), qui ne contient donc
pas Bf(p)(p).
Donc Bf(p)(p) est incluse dans F, mais n'est pas incluse dans une plus grande boule Br'(p') qui serait incluse dans F. On obtient donc la :
2ème définition : Le squelette de distance d'une figure F est formé de tous les points p de F qui sont centres d'une boule incluse dans F, maximale pour l'inclusion : pour un rayon r, Br(p) est incluse dans F, mais pour un point p' de F et un rayon r'>r, on ne peut pas avoir à la fois Br(p) incluse dans Br'(p') et Br'(p') incluse dans F.
Si on écrit S1 pour le squelette de F selon la 1ère définition, et S2 pour celui selon la 2ème définition, il est clair que S1 est inclus dans S2 (c'est ce que nous avons expliqué plus haut). Cependant les deux squelettes ne sont pas nécessairement égaux. Par exemple, dans le cas du rectangle, les coins appartiennent à S2, mais pas à S1. De même, quand le bord de la figure atteint un maximum de courbure en un point q, le rayon de courbure (inverse de la courbure) atteint un minimum r, et il y aura un point de S2 \ S1 à distance r de q, comme illustré ci-dessous :
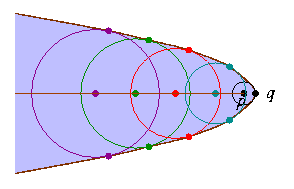
Chaque point x du squelette est centre d'une boule touchant le bord de la figure F en deux points y1 et y2, sauf le point p à son extrémité, centre d'une boule de rayon f(p), qui touche le bord de F en un seul point q ; en fait, quand x tend vers p, y1 et y2 tendront tous deux vers q. Ici p satisfait la 2ème définition, mais pas la 1ère, donc p appartient à S2 \ S1.
On peut montrer (par exemple Matheron, 1988), que S2 est inclus dans la fermeture topologique de S1, en d'autres termes un point de S2 \ S1 est un point limite de S1.
Quand un front de flamme se déplace dans le temps, la distance au bord f(p) = d(p,ðF) a une pente de 1 dans la direction perpendiculaire au front. Là où deux fronts se rejoignent, on a une telle pente dans deux directions ; mathématiquement parlant, le gradient (la pente) n'est pas défini en ce point. On peut représenter géométriquement la fonction f dans l'espace à trois dimensions, le plan horizontal étant celui de l'image, et la hauteur correspondant à la valeur de f ; en d'autres termes on prend les points (p1, p2, f(p1, p2)) pour tous les points p = (p1, p2) de la figure. Nous illustrons cela ci-dessous pour la figure en forme de rectangle vue plus haut, on voit que f forme un "toit" de pente 1, et les arêtes du toit correspondent aux points du squelette.
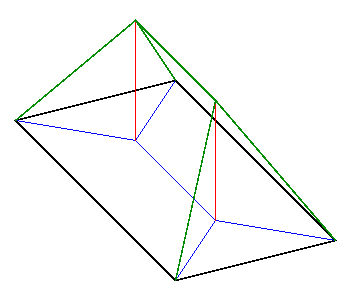
Ceci conduit ainsi à la :
3ème définition : Le squelette de distance d'une figure F est le lieu des points p de F où la transformée de distance f(p) = d(p,ðF) (de marqueur ðF dans le masque F) n'est pas différentiable.
Finalement, on choisira la 2ème définition, qui est celle qui se prête le mieux à la description des propriétés du squelette, ainsi qu'à la généralisation à une autre métrique que la distance euclidienne, ou à un espace discret.
Le squelette de distance est aussi appelé axe médian.
Le squelette de distance possède effectivement les 3 propriétés que nous avons requises plus haut, à savoir : il est formé de lignes sans épaisseur, centré dans la figure, il a la même forme générale et la même topologie que la figure.
Le fait d'être formé de lignes sans épaisseur, et celui d'être centré, ne nécessitent pas d'explication. Pour ce qui est de la préservation de la forme générale de la figure, le concept de forme est assez vague, mais on peut comprendre qu'à une partie allongée de la figure correspondra dans le squelette une longue ligne au milieu de celle-ci.
Pour la topologie, on peut au contraire être très précis. La topologie d'une figure euclidienne bornée est formée de l'arborescence des composantes connexes de la figure et du fond, tout comme dans le cas discret, sauf qu'on considère la même connexité (topologique euclidienne) sur la figure et sur le fond. Le squelette aura la même arborescence, plus précisément on aura une bijection entre l'arborescence de la figure et celle du squelette, donnée comme suit :
Cette correspondance préserve l'adjacence entre composantes de la figure et du fond (ou du squelette et de son complémentaire), donc elle induit un isomorphisme entre les deux arborescences (bijection entre les sommets, qui donne une bijection entre les arêtes). C'est ce que nous illustrons ci-dessous :
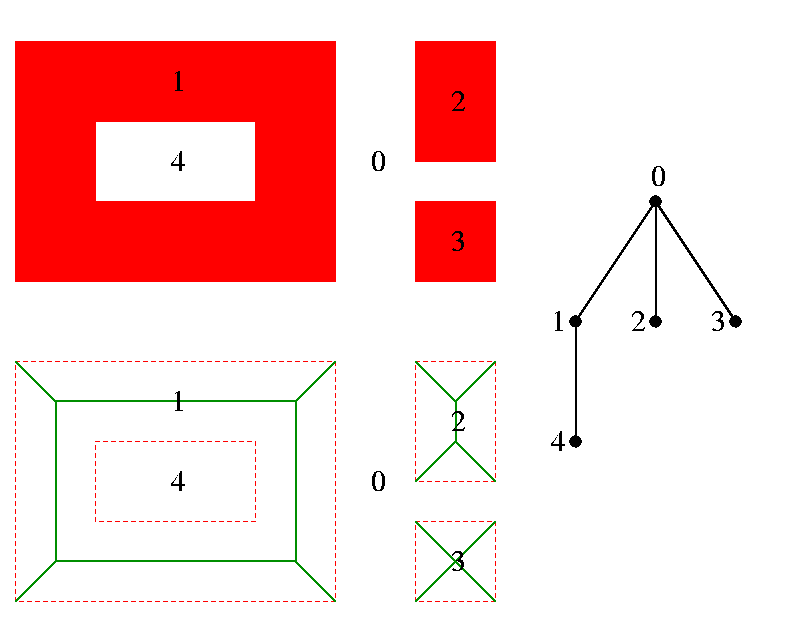
En haut, les composantes connexes de la figure et du fond. En bas, les
composantes correspondantes du squelette et de son
complémentaire. A droite, l'arborescence des composantes
connexes de la figure et du fond, et aussi du squelette et de son
complémentaire.
Le squelette de distance est non robuste. En effet, une aspérité du contour, aussi petite soit-elle, peut conduire à une nouvelle branche du squelette. C'est ce que nous illustrons ci-dessous avec une petite pointe sur le côté d'un rectangle ; quand la taille de cette pointe tend vers zéro, la nouvelle branche du squelette restera grande :
Notons finalement qu'à partir du squelette de distance S et de la fonction f donnant la distance au bord de la figure F, f(p) = d(p,ðF), on peut reconstruire F. En effet, F est la réunion des boules Bf(p)(p) pour tous les points p de S.
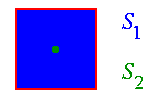
Si on remplace la distance euclidienne par une distance de chanfrein, une partie importante de ce que nous avons dit plus haut devient faux. Tout d'abord le squelette S1 selon la 1ère définition n'est pas nécessairement inclus dans S2, celui selon la 2ème définition. Par exemple, avec la 8-distance, pour un carré aux côtés parallèles aux axes, S1 forme tout l'intérieur du carré, alors que S2 comprend uniquement son centre.
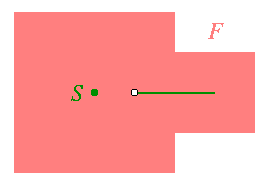
Si on se tient à la 2ème définition, comme indiqué plus haut, alors le squelette ne conserve pas la topologie de la figure, comme on le voit dans l'exemple ci-contre. Pour la 8-distance, le squelette S (selon la 2ème définition) de la figure F consiste en un segment (excluant une extrémité, marquée par un petit cercle vide), et un point isolé ; ainsi F est connexe, mais S ne l'est pas.
Ces problèmes sont à rapporter à ceux qu'on obtient pour le squelette par zones d'influences avec une distance de chanfrein, et ils ont la même cause : le cercle correspondant à une distance de chanfrein est un polygone.
Par contre la propriété de reconstructibilité, à savoir que F est la réunion, pour tous les points p de S, des boules Bf(p)(p), où f(p) = d(p,ðF), reste toujours valable. En effet, une telle boule Bf(p)(p) (pour un point p de S) est toujours incluse dans F, tandis que tout point q de F appartient à la boule B0(q), qui sera incluse dans une boule maximale Bf(p)(p) pour un point p de S.
On voit donc qu'il n'y a aucun avantage à utiliser une distance de chanfrein pour le squelette d'une figure euclidienne. Par contre, si on se met dans le plan discret Z2 au lieu du plan euclidien R2, les distances de chanfrein se justifient par l'algorithme séquentiel pour la transformée de distance. On peut utiliser la 2ème définition du squelette de distance : c'est l'ensemble des pixels centres d'une boule incluse dans la figure, maximale pour l'inclusion.
Ici, f(p) sera la distance de p au bord intérieur de la figure. Pour la 4- ou la 8-distance, f(p) = d(p,B) - 1, où B est le fond, c.-à-d. le complémentaire de la figure. Par ailleurs, f(p) est le rayon de la plus grande boule centrée en p et incluse dans la figure.
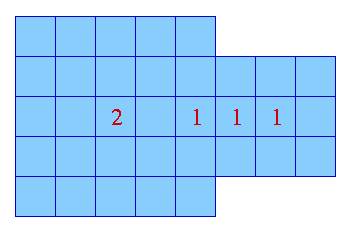
Comme dans le cas euclidien, le squelette de distance de chanfrein d'une figure discrète ne préserve pas la topologie de cette figure. Nous illustrons ceci dans le cas de la 8-distance ; dans la figure ci-dessous, les points p du squelette sont indiqués avec la valeur f(p).
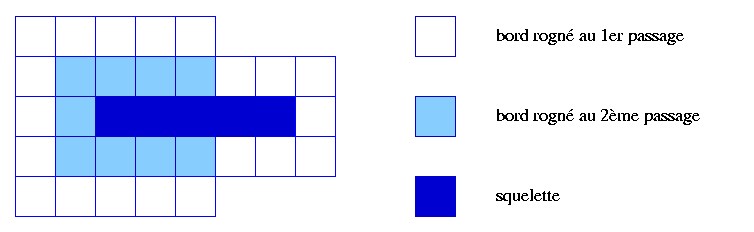
Ceci conduit à adopter une autre approche pour construire le squelette d'une figure discrète. L'analogie avec le feu de prairie indique un processus d'amincissement progressif de la figure obtenu en rognant récursivement son bord. Cependant, on introduira dans l'opération qui rogne le bord une condition de préservation de la topologie. Ainsi, la figure ci-dessus serait squelettisée après deux passages de l'opération rognant le bord tout en conservant la topologie, comme illustré ci-dessous :