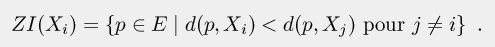
Soit E un espace de points (E = Rdim ou Zdim, dim = 2, 3, ...), muni d'une distance (métrique) d. Soient n parties X1, ..., Xn de E, appelées marqueurs, qu'on suppose mutuellement disjointes (l'intersection de Xi et de Xj est vide pour i différent de j). Chaque marqueur Xi (i = 1, ..., n) détermine une zone d'influence, formée de tous les points de E strictement plus proches de Xi que de tout autre marqueur :
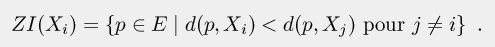
Comme on requiert l'inégalité stricte de distances d(p,Xi) < d(p,Xj), il s'agit ici de zones d'influence au sens strict. On peut aussi définir les zones d'influence au sens large, en remplaçant l'infériorité stricte < par l'infériorité ou égalité :
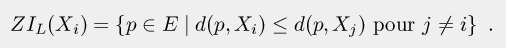
Dans le cas euclidien (E = Rdim, et d étant la distance euclidienne), la zone d'influence au sens large ZIL(Xi) contient la zone d'influence au sens strict ZI(Xi), plus les frontières de celle-ci avec les zones d'influence voisines.
Le squelette par zones d'influence de marqueurs X1, ..., Xn, aussi appelé SKIZ (de l'anglais SKeleton by Influence Zones), est formé de tous les points frontières entre les différentes zones d'influence. On le notera SKIZ(X1, ..., Xn). Il comprend tous les points n'appartenant à aucune zone d'influence au sens strict, en d'autres termes tous les points appartenant à au moins deux zones d'influence au sens large :
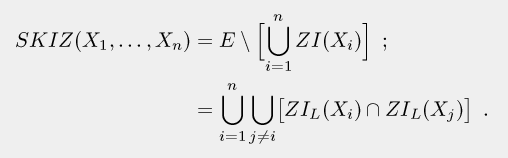
En fait, il est constitué de tous les points p tel qu'il existe i, j distincts (parmi 1, ..., n) pour lesquels
d(p,Xi) = d(p,Xj) = min { d(p,Xt) | t = 1, ..., n }.
Nous illustrons ci-dessous le SKIZ euclidien à deux dimensions (E = R2, et d est la distance euclidienne) de trois marqueurs constitués chacun d'un unique point. Le SKIZ est formé de portions des trois médiatrices du triangle dont ces trois points sont les sommets :
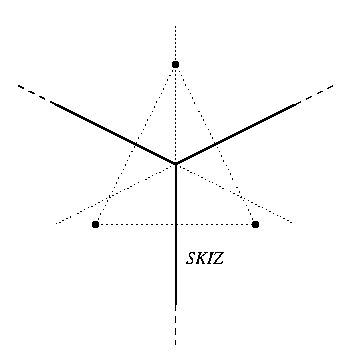
Pour des marqueurs ponctuels, le SKIZ euclidien est le diagramme de Voronoi. Le calcul de ce diagramme est un problème classique en géométrie algorithmique. En traitement d'images, on considèrera au contraire des marqueurs quelconques, mais dans un espace discret (E = Zdim), et plutôt que d'utiliser des méthodes de géométrie algorithmique, on recherchera des algorithmes basés sur la transformée de distance.
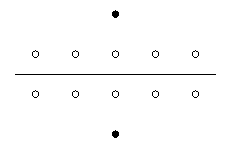
Dès qu'on remplace l'espace euclidien Rdim par l'espace discret Zdim, des problèmes apparaissent. Ainsi, la frontière entre deux zones d'influence passe généralement entre les pixels. Prenons dans Z2 deux marqueurs formés chacun d'un pixel, de telle sorte que ces deux pixels soient sur une même colonne verticale, et à distance impaire l'un de l'autre. Le SKIZ sera alors une ligne horizontale passant exactement au milieu de deux lignes de pixels, comme illustré ci-contre.
Une solution possible à ce problème est d'insérer des inter-pixels ou points à coordonnées entières plus un demi, c.-à-d. de plonger Zdim dans (½Z)dim. Chaque fois que deux pixels 8-adjacents appartiennent à des zones d'influence distinctes, l'interpixel situé au milieu des deux sera marqué comme point du SKIZ.
Un problème plus grave est lié à l'utilisation d'une distance de chanfrein (que ce soit dans l'espace euclidien Rdim ou l'espace discret Zdim) : on obtient souvent un SKIZ épais. Par exemple en dimension 2, la médiatrice entre deux points n'est pas nécessairement une ligne, mais elle peut contenir des plages épaisses du plan. C'est ce qui se passe pour la 4-distance avec deux points en diagonale, et aussi pour la 8-distance avec deux points à la verticale ou l'horizontale :
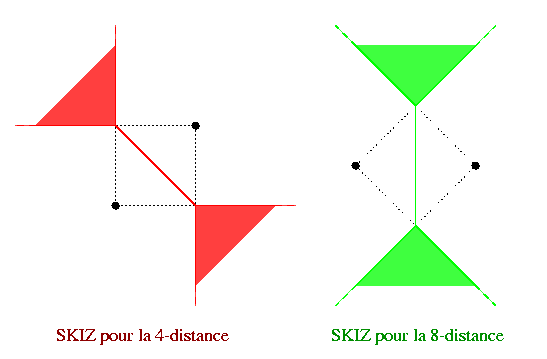
Ce problème se pose avec n'importe quelle distance de chanfrein, pas uniquement d4 et d8. Il provient du fait que le cercle (lieu des points à distance constante d'un centre) est un polygone (en 2 dimensions) ou un polytope (en 3 dimensions), donc dès qu'on prend deux points p et q tels que le segment pq est parallèle à une des faces de ce cercle, pour un rayon r supérieur à la moitié de la distance entre p et q, les deux cercles de rayon r centrés respectivement en p et q auront une intersection épaisse (par exemple en 2 dimensions, l'intersection de ces deux cercles est formée de deux segments), et de telles intersections épaisses sous-tendent des zones épaisses du SKIZ. C'est ce que nous illustrons ci-dessous pour la 8-distance, en comparaison avec la distance euclidienne :
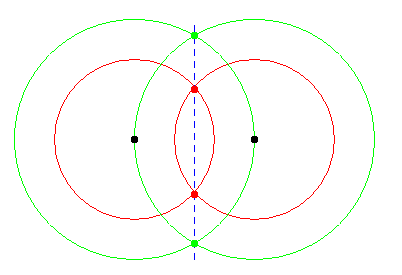
Deux cercles euclidiens s'intersectent en deux points.
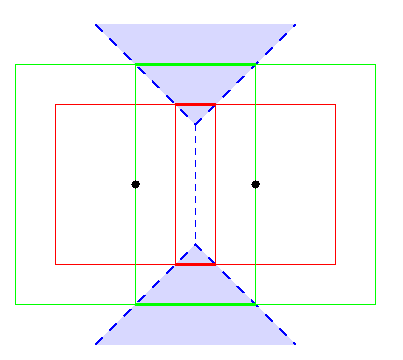
Deux cercles pour la 8-distance peuvent s'intersecter en deux
segments.
Une solution est de construire le SKIZ algorithmiquement en propageant en parallèle une zone d'influence à partir de chaque marqueur ; quand deux zones provenant de marqueurs distincts se rencontrent en un point, on le marque "digue", ce qui signifie qu'une zone ne peut pas se propager à partir d'un tel point, en particulier elle ne peut pas le traverser. Nous illustrons la différence entre ce SKIZ algorithmique et le SKIZ géométrique en dimension 2 pour la 4-distance avec deux marqueurs ponctuels en diagonale :
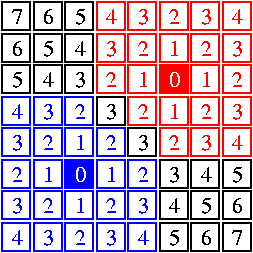
A gauche :
Deux marqueurs ponctuels (en bleu et en rouge), leurs zones
d'influences au sens strict (pixels ayant leur bord de même
couleur), et le SKIZ (pixels bordés de noir). Au milieu de
chaque pixel est écrite la distance au marqueur le plus
proche.
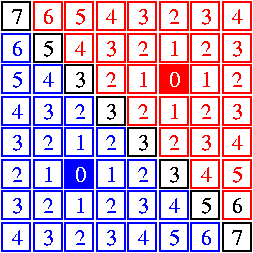
A droite :
Construction algorithmique du SKIZ par propagation. Les marqueurs
initient les zones d'influence au temps 0. Au temps t, un
pixel d'une zone d'influence propage sa marque de zone et le temps
t + 1 à ses voisins non marqués. Si les deux
zones se propagent sur un pixel, celui-ci est marqué
"digue" et ce pixel ne propage pas de marque vers ses
voisins.
On pourrait aussi utiliser un couple de deux distances (par exemple la 4- et la 8-distances pour dim = 2) ordonné lexicographiquement. Soient d1 et d2 les deux distances, on définit la distance [d1,d2] par
[d1,d2](p,q) = (d1(p,q),d2(p,q)),
où les couples de valeurs (a1,a2) que prend [d1,d2] sont ordonnés lexicographiquement : (a1,a2) < (b1,b2) ssi a1 < b1 ou a1 = b1 et a2 < b2. Alors le SKIZ défini comme plus haut (complément de l'union des zones d'influence au sens strict, ou union des intersections entre zones d'influence au sens large) est épars, on le redéfinit donc comme l'union des frontières entre zones d'influence au sens strict.
Le squelette par zones d'influence peut servir à délimiter des régions dont une partie intérieure est donnée par des marqueurs. Il est utilisé par certains algorithmes de segmentation par croissance de régions, en particulier la ligne de partage des eaux. On peut décomposer une figure binaire en ses différents constituants avec le SKIZ construit en prenant comme marqueurs les maxima locaux de la transformée de distance par rapport au complément de cette figure.