Cr = { p 
E |
d(p,C) 
r } , où
d(p,C) = min {
d(p,x) | x C } .
Un algorithme de détection d'arêtes ne produit en général qu'une partie des contours des objets. Comme ces contours ne sont pas fermés, ils ne permettent pas de séparer les objets. Nous montrons ci-contre le contour non fermé d'un rectangle.
Quand ces contours sont épars (c.-à-d. deux morceaux de contours distincts ne peuvent être proches), on peut fermer ces contours au moyen de la transformée de distance et de la réduction topologique.
On suppose que deux morceaux de contours distincts sont séparés par une distance d'au moins 2r, où r > 0. La dilatation du contour C par la boule Br de rayon r donne l'ensemble Cr de tous les pixels dont la distance à C est au plus r :
Cr = { p
Pour une distance de chanfrein satisfaisant les conditions de
Montanari, l'ensemble Cr peut être
obtenu en appliquant l'algorithme de
transformée de distance au marqueur C et en
sélectionnant tous les pixels où cette
transformée donne une valeur
r.
Nous illustrons ci-contre la construction de Cr (en rouge) pour la distance euclidienne. On voit que deux morceaux d'un contour distants l'un de l'autre de moins que 2r se retrouveront dans la même composante connexe de Cr. De plus, Cr aura la même forme générale que C, mais sera épais.
On appliquera donc à Cr une réduction topologique préservant le contour initial C. En d'autres termes, on retire successivement des pixels de Cr, sous la double contrainte qu'un tel retrait ne modifie pas la topologie, et qu'un pixel de C ne puisse pas être retiré ; ce processus s'arrête quand il n'est plus possible d'enlever de pixel sans violer une des deux contraintes. Cette réduction est supposée isotrope, c.-à-d. de façon égale dans toutes les directions. On obtient alors un ensemble mince D contenant C, où deux morceaux de contours dans C distants de moins que 2r seront joints par une ligne. Nous illustrons cela ci-contre (avec Cr est en rose, et D \ C en vert), ainsi D sera la fermeture du contour C.
Dans le cas où les contours ne sont pas épars (des
contours distincts peuvent être proches), cette méthode
induira des jonctions entre certains contours. Nous illustrons cela
pour un contour C formé de lignes fracturées
horizontales :
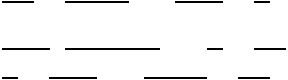
Le contour C.
En rouge le dilaté Cr de
C par la boule Br de rayon
r.
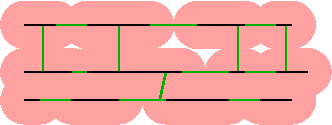
En rose Cr, et en vert D \
C, où D est la réduction topologique
de Cr préservant C.
Notons également que rien ne garantit que les segments rajoutés pour fermer le contour ne soient rectilignes, ils peuvent être fortement courbés.
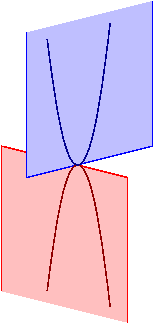
Nous présentons donc une autre méthode due à Milgram et Cocquerez (1986), basée sur une répétition de l'ajout au contour des points selle de la transformée de distance.
On appelle un point selle d'une fonction à deux variables un point réalisant un minimum local strict de cette fonction dans une direction, et un maximum local strict dans la direction perpendiculaire, cf. ci-contre.
On remarquera que, comme illustré ci-dessous, pour un marqueur formé de deux segments parallèles ou incidents, la transformée de distance n'a aucun point selle :
A gauche, le segment médian bleu (sans ses
extrémités) réalise un maximum local de la
transformée de distance dans la direction verticale, mais
celle-ci est constante sur ce segment, donc n'a pas de minimum local
strict. A droite, la transformée de distance n'a de maximum
local dans aucune direction.
Par contre un point selle existe entre deux concavités ou
extrémités se faisant face :
En rouge, le contour, en bleu le point selle, et en pointillés
les deux directions
selon lesquelles la transformée de distance a un maximum et un
minimum stricts.
On applique ainsi l'algorithme suivant pour fermer un contour C :
Répéter :
- calculer la transformée de distance de C ;
- rajouter à C les points selle de la transformée ;
jusqu'à ce qu'il n'y ait plus de point selle à ajouter.
Pour le contour formé de lignes fracturées horizontales vu plus haut, les deux premières itérations donnent :
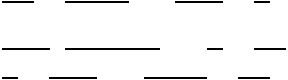
Le contour initial.
1ère itération de l'algorithme (pixels rajoutés
en rouge).
2ème itération de l'algorithme (pixels rajoutés
en vert).
Pour éviter de prendre en compte des points selle entre deux
contours distants, on peut dans l'algorithme restreindre les points
selle à ceux dont la distance au contour C est
inférieure à un seuil s. Par ailleurs, pour
limiter le nombre d'itérations, on peut définir une
distance minimum h, et pour tout point selle p tel
que d(p,C) < h, on tracera un
segment entre p et chaque point q C tel que
d(p,q) =
d(p,C) ; ainsi cela fermera le contour
autour de p, et évitera à l'itération
suivante de considérer les points selle entre p et
C.
Quand trois extrémités de contours forment les sommets d'un triangle, l'algorithme tendra à remplir ce triangle. C'est ce que nous illustrons ci-dessous à gauche, où le contour initial est en noir, et les différentes couleurs correspondent aux points selle ajoutés lors des 3 premières itérations (t = 1, 2, 3). Si on veut éviter cela et ne remplir que le bord du triangle, lors de chaque itération t on restreindra l'ajout de points selle à ceux tels que parmi les points du contour les plus proches, il y en a au moins un qui fasse partie du contour initial, ou ait été ajouté comme point selle lors de l'itération t - 2. Voir ci-dessous à droite.
Tout comme pour le SKIZ, cette approche, définie dans l'espace euclidien pour la distance euclidienne, posera des problèmes pour un espace discret ainsi que pour une distance de chanfrein :
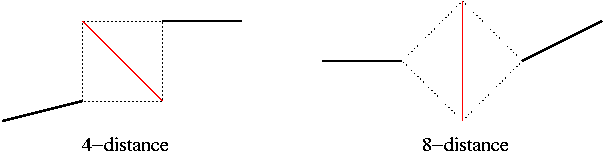
Le segment médian rouge (sans ses extrémités)
réalise un maximum local de la transformée de distance
dans la direction perpendiculaire, mais celle-ci est constante sur ce
segment, donc n'a pas de point selle.
Un solution serait de considérer deux distances de chanfrein (par exemple la 4- et la 8-distance) et de prendre les points selle pour les deux transformées de distance correspondantes.