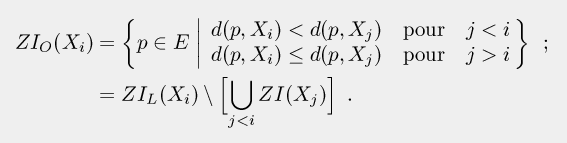
Supposons l'espace discret à deux dimensions (E = Z2), avec une distance d de chanfrein satisfaisant les conditions de Montanari. Soit S un masque rectangulaire dans E, et n marqueurs X1, ..., Xn inclus dans S. On peut construire dans le masque S les zones d'influence et le SKIZ des marqueurs, grâce à une variante de l'algorithme de transformée de distance. Celui-ci calculait pour tout pixel p de S une valeur f(p) égale à la distance de p à un marqueur R. Ici f(p) sera la distance de p au plus proche des marqueurs X1, ..., Xn (en d'autres termes, la distance de p à la réunion de ces marqueurs), mais l'algorithme associera aussi à p un entier m(p) entre 1 et n, qui est le numéro du marqueur le plus proche de p (donc m(p) = i pour d(p,Xi) = f(p)).
S'il y avait deux numéros distincts i et j tels que d(p,Xi) = d(p,Xj) =f(p), alors p appartiendrait au SKIZ, et il faudrait normalement attribuer à m(p) une valeur spéciale (par exemple 0 ou n + 1) correspondant au SKIZ. Les problèmes mentionnés précédemment (SKIZ passant entre les pixels, ou épais), font qu'il est plus simple d'adopter la démarche suivante, provenant du premier algorithme de Meyer pour la ligne de partage des eaux, que nous appellerons Meyer-1 :
Si on considère uniquement les points 1 et 2 ci-dessus, c.-à-d. qu'on partitionne le masque en zones d'influence sans SKIZ, alors ces zones d'influence seront intermédiaires entre les zones d'influence au sens strict ZI(Xi) et les zones d'influence au sens large ZIL(Xi). Nous les appelons zones d'influence ordonnées et les notons ZIO(Xi). Elles sont définies comme suit : la zone d'influence ordonnée d'un marqueur est formée de tous les pixels strictement plus proches de ce marqueur que de tout autre marqueur de numéro inférieur, et plus proches ou à même distance de ce marqueur que de tout autre marqueur de numéro supérieur. Formellement :
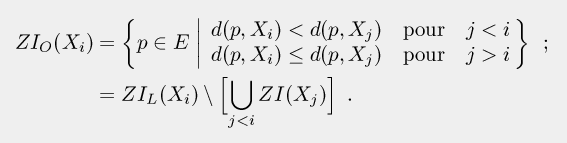
On a ainsi :
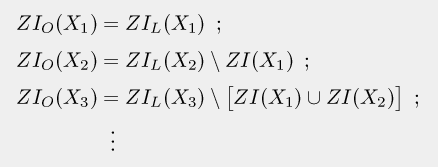
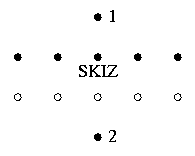
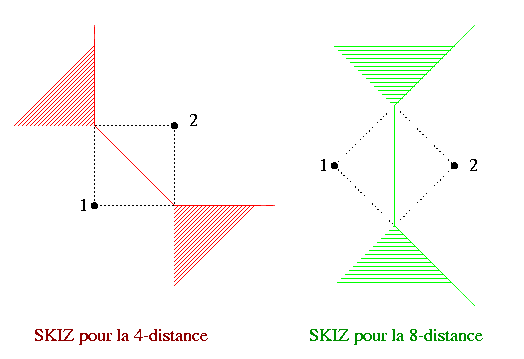
Si on construit le SKIZ avec tous les pixels ayant un voisin appartenant à une zone d'influence ayant un numéro supérieur (cfr. le point 3 ci-dessus), alors les problèmes du SKIZ non-euclidien se résolvent de la façon suivante. Premièrement, le SKIZ ne pourra plus passer entre deux pixels, dans ce cas il sera dévié du côté de celui appartenant à la zone d'influence ayant le plus petit numéro (voir ci-contre). Deuxièmement, on n'aura plus de SKIZ épais ; une zone épaisse du SKIZ sera affectée à la zone d'influence de plus petit numéro, sauf son bord (non épais) avec l'autre zone. Ceci est illustré ci-dessous, où la zone épaisse du SKIZ (au sens originel) est hachurée, tandis que le SKIZ des zones d'influence ordonnées forme une ligne :
L'algorithme de transformée de distance s'adapte alors au calcul des zones d'influence ordonnées :
m et f sont deux fonctions définies sur S.
H est un nombre considéré comme "infini".(0) Initialisation
Pour chaque p dans S on pose
f(p) := 0 et m(p) := i si p appartient au marqueur Xi (i = 1, ..., n),
f(p) := H et m(p) := n+1 si p n'appartient à aucun de ces marqueurs.(1) Balayage dans l'ordre direct :
Pour le pixel p allant du premier au dernier, faire
x := min { f(q) + M¯p(q) | q dans V¯(p) } ;
m(p) := min { m(q) | q dans V¯(p), f(q) + M¯p(q) = x } ;
f(p) := x .(2) Balayage dans l'ordre inverse :
Pour le pixel p allant du dernier au premier, faire
x := min { f(q) + M+p(q) | q dans V+(p) } ;
m(p) := min { m(q) | q dans V+(p), f(q) + M+p(q) = x } ;
f(p) := x .A la fin de l'algorithme, pour chaque pixel p du masque S, m(p) donnera le numéro i de la zone d'influence ordonnée ZIO(Xi) à laquelle il appartient, et f(p) donnera la distance de p à ZIO(Xi).
Les remarques que nous avons données concernant l'algorithme de transformée de distance restent valables ici.
Nous décrivons brièment deux autres approches qui construisent à des zones d'influence et un SKIZ. Nous les déconseillons, car leur comportement effectif cause des problèmes. Ici, pour un pixel p, la valeur de m(p) sera un entier m(p) entre 0 et n, où m(p) = 0 signifie que p fait partie du SKIZ, tandis que pour m(p) = i > 0, p fait partie de la zone d'influence du marqueur Xi.
Dans l'approche issue du second algorithme de Meyer pour la ligne de partage des eaux, que nous appellerons Meyer-2 :
L'algorithme décrit plus haut doit alors être modifié dans les étapes (1) et (2) de balayages dans l'ordre direct et dans l'ordre inverse. Nous ne décrivons ici que l'étape (1), l'autre est semblable :
(1) Balayage dans l'ordre direct :
Pour le pixel p allant du premier au dernier, faire
S'il existe au moins un q dans V¯(p) tel que m(q) > 0 Alors :x := min { f(q) + M¯p(q) | q dans V¯(p), m(q) > 0 } ;
A := { m(q) | q dans V¯(p), m(q) > 0, f(q) + M¯p(q) = x } ;
Si |A| = 1 Alors m(p) := élément de A Sinon m(p) := 0 ;
f(p) := x .
Le problème est que si tous les chemins les plus courts d'un pixel p à son marqueur le plus proche passent par des portions du SKIZ, alors les valeurs de f(p) et m(p) ne seront pas correctement mises à jour. Dans certains cas, f(p) et m(p) garderont les valeurs de l'initialisation.
Il y a une dernière approche construisant le SKIZ. Contrairement à celle de Meyer-2, il n'y a pas de restriction sur les pixels propageant l'information de distance. Elle a été utilisée dans l'algorithme de Soille et Vincent pour la ligne de partage des eaux (quoique leur algorithme suive un schéma différent). Nous donnons ici la modification de l'étape (1) de l'algorithme (balayage dans l'ordre direct), celle de l'étape (2) (balayage dans l'ordre inverse) est semblable :
(1) Balayage dans l'ordre direct :
Pour le pixel p allant du premier au dernier, faire
x := min { f(q) + M¯p(q) | q dans V¯(p) } ;
A := { m(q) | q dans V¯(p), f(q) + M¯p(q) = x } ;
Si |A| = 1 Alors m(p) := élément de A Sinon m(p) := 0 ;
f(p) := x .
Cette approche construira des SKIZ épais, et elle a tendance à propager le SKIZ à l'intérieur des zones d'influence.
Lorsque le SKIZ passe entre deux pixels (voir plus haut), les deux approches avec SKIZ ne marqueront aucun de ces deux pixels comme membre du SKIZ. Il faudra donc compléter le SKIZ de la même manière que pour l'approche Meyer-1. En conclusion, ces deux approches n'ont aucun avantage, mais uniquement des inconvénients, par rapport à l'approche Meyer-1 sans SKIZ.