On considère des images discrètes définies sur un ensemble discret de points E (par exemple E est une grille rectangulaire), et dont les niveaux de gris sont des entiers compris entre le niveau de gris minimum 0 et le niveau de gris maximum M (par exemple, M = 255). Donc une telle image peut être vue comme une fonction I de E vers {0, ..., M}, associant à un point p de E le niveau de gris I(p).
Pour un ensemble fini X, nous écrivons #X pour sa taille (le nombre d'éléments de X). Nous posons n= #E.
L'histogramme de l'image I est la fonction HI définie sur l'intervalle de niveaux de gris {0, ..., M} et à valeurs entières non-négatives, associant à tout niveau de gris g le nombre de points dans E ayant le niveau de gris g dans l'image I.
HI(g) = #{p | I(p) = g}.
Par conséquent, étant donnés deux niveaux de gris a et b (avec a < b) de l'intervalle {0, ..., M}, le nombre de points p de E dont le niveau de gris est compris entre a et b est donné par la somme HI(a) + ... + HI(b). En particulier, on a
HI(0) + ... + HI(M) = #E = n.
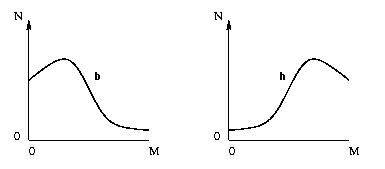
La présentation visuelle de l'histogramme d'une image permet de se rendre compte rapidement des défauts de contraste dans cette image.

Par exemple dans l'illustration ci-dessus,
Bien sûr, la qualité visuelle d'un image ne dépend pas uniquement de son histogramme, mais surtout de la nature et du but de l'image. Par exemple, dans une image médicale, on cherchera à mettre en évidence les structures anatomiques ou pathologiques d'intérêt, au dépens des autres. Dans une photo d'identité il importe d'établir un bon contraste entre la tête et le fond.
Pour remédier aux défauts de contraste d'une image, on peut appliquer un rehaussement des niveaux de gris ; la fonction de rehaussement doit être choisie en fonction du défaut de l'histogramme.
On peut également appliquer une forme de rehaussement automatique appelée égalisation d'histogramme. Elle consiste à calculer à partir de l'histogramme HI de l'image I une fonction de rehaussement des niveaux de gris f telle que l'image rehaussée J, définie par J(p) = f(I(p)), ait son histogramme HJ se rapprochant le plus possible d'une fonction "plate".
En pratique, étant donnée la nature discrète de l'espace de points et de l'échelle de niveaux de gris, il est impossible d'obtenir un histogramme "plat" pour l'image rehaussée. En effet, si l'image initiale I comporte k niveaux de gris (où k << M), l'image rehaussée J en comprendra au plus k ; elle peut même en comporter moins, car on peut avoir deux niveaux de gris distincts g et g' présents dans l'image I, tels que f(g) = f(g') ; or un histogramme "plat" signifie que tous les niveaux de gris sont présents en même nombre dans l'image.
L'égalisation d'histogramme d'une image discrète utilise une discrétisation de la formule obtenue dans le cas continu pour obtenir un histogramme entièrement plat. Nous définissons l'histogramme cumulatif de l'image I comme la fonction CI définie sur l'intervalle de niveaux de gris {0, ..., M} et à valeurs entières non-négatives, associant à tout niveau de gris g le nombre de points dans E ayant un niveau de gris inférieur ou égal à g dans l'image I. On a donc:
CI(g) = HI(0) + ... + HI(g),
et on peut donc obtenir CI par l'itération suivante:
CI(0) = HI(0), et
CI(g) = CI(g - 1) + HI(g) pour g = 1, ..., M.
En particulier CI(M) = #E = n. On applique alors à l'image I la fonction de rehaussement des niveaux de gris f définie par
f(g) = M CI(g) / n (arrondi à l'entier le plus proche).
Notons que CI(g) / n est la proportion de points de E ayant un niveau de gris inférieur ou égal à g dans l'image I, donc le niveau de gris f(g) sera la fraction de M correspondant à cette proportion. On a
f(0) = M HI(0) / n et f(g) - f(g - 1) = M HI(g) / n pour g = 1, ..., M. En particulier f(M) = M.
L'effet de cette fonction de rehaussement f est de mettre à gauche de chaque niveau de gris un écart dont la taille est proportionnelle au nombre de points ayant ce niveau de gris dans l'image I. Donc tout niveau de gris fortement représenté dans l'image se verra écarté des niveaux de gris plus sombres. En pratique l'image aura un aspect où les zones claires, moyennes et sombres s'équilibreront.
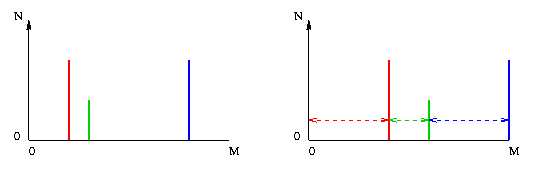
Le fait que f(g) soit placé à droite d'un intervalle de taille M HI(g) / n peut induire un déséquilibre dans l'image à histogramme égalisé quand certains niveaux de gris représentent une fraction importante des pixels de l'image. C'est ce que nous illustrons (ci-dessous à gauche) avec l'histogramme d'une image ayant en tout 3 niveaux de gris distincts, représentant chacun respectivement 40%, 20% et 40% de l'image. Dans l'histogramme égalisé (ci-dessous à droite), on voit que les niveaux de gris se mettront aux percentiles 40%, 60% et 100% de l'échelle de niveaux de gris.
Si on avait appliqué le dual de l'égalisation d'histogramme (c.-à-d. faire un négatif de l'image, égaliser l'histogramme du négatif, puis refaire un négatif), la fonction de rehaussement serait
f(g) = M CI(g - 1) / n (arrondi à l'entier le plus proche),
où f(0) = M CI(-1) / n = 0.
C'est ce que nous illustrons (ci-dessous à gauche) avec l'histogramme de l'exemple précédent, et dans l'histogramme égalisé les 3 niveaux de gris se mettront aux percentiles 0%, 40% et 60% de l'échelle de niveaux de gris.
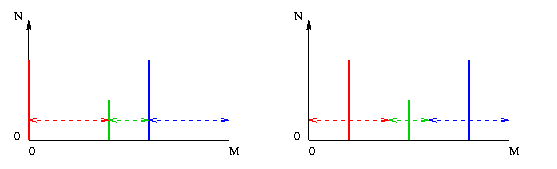
Finalement, on pourrait prendre la moyenne des deux, à savoir
f(g) = M [CI(g - 1) + CI(g)] / 2n (arrondi à l'entier le plus proche).
Ceci est illustré (ci-dessus à droite) pour le même exemple, et les 3 niveaux de gris se mettront aux percentiles 20%, 50% et 80% de l'échelle de niveaux de gris, ce qui est plus équilibré.
Attention ! Dans une image bien contrastée, l'égalisation d'histogramme peut donner une image de qualité visuelle moindre, comme dans l'exemple ci-dessous: