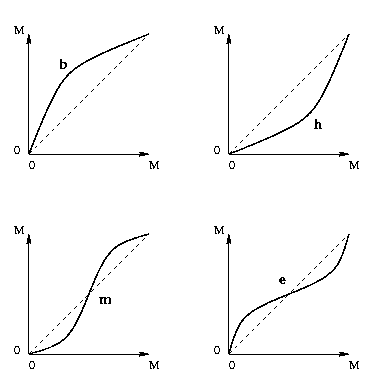
Soit M le niveau de gris maximum (par exemple, M = 255). On suppose que le niveau de gris minimum est 0. Le rehaussement consiste à appliquer aux niveaux de gris de l'image une fonction croissante f telle que f(0) = 0 et f(M) = M.
Le graphe de f indique le type de rehaussement appliqué à l'image: les plages de niveaux de gris où la pente de f est forte seront rehaussées au dépens de celles où cette pente est faible.
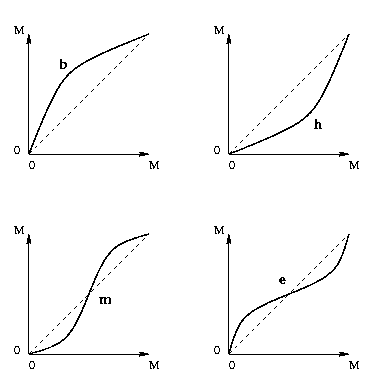
Par exemple dans l'illustration ci-dessus, b rehausse les bas niveaux de gris (zones sombres), tandis que h rehausse les hauts niveaux de gris (zones claires), m rehausse les niveaux de gris moyens, et e rehausse les niveaux de gris extrêmes.
Soit f une fonction de rehaussement des niveaux de gris. L'inverse de f est la fonction f -1 définie par y = f -1(x) ssi x = f(y). Le graphe de f -1 est obtenu à partir de celui de f par symétrie par rapport à la diagonale y = x. Comme la pente de f -1 est l'inverse de celle de f, l'effet de rehaussement de f -1 est l'opposé de celui de f : là où f augmente les contrastes, f -1 les diminuera, et vice versa. Le dual de f est la fonction f * obtenue en appliquant successivement un négatif, f, puis encore un négatif, en d'autres termes
f *(x) = M - f(M - x).
Le graphe de f * est obtenu à partir de celui de f par symétrie centrale (rotation de 180°). La pente de f * en x est celle de f en M - x, donc l'effet de rehaussement de f * sur une plage de niveaux de gris sera celui de f sur la plage opposée. Notons enfin f ~ = (f -1)* =(f *)-1, le dual inverse de f, dont le graphe est obtenu à partir de celui de f par symétrie par rapport à la diagonale y = M - x.
Les relations d'inverse, de dual, et de dual inverse sont symétriques, c.-à-d. (f -1)-1 = (f *)* = (f ~)~ = f.
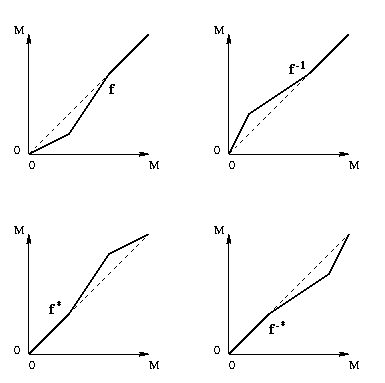
Nous illustrons dans la figure ci-dessus cette construction à partir d'une fonction f (en haut à gauche) de son inverse f -1 (en haut à droite), son dual f * (en bas à gauche), et de son dual inverse f -* (en bas à droite). On peut comparer les effets de chacune des quatre sur les contrastes :
Dans la première illustration, on avait h = b -1 et e = m -1 ; de plus, h = b *, tandis que m * = m et e * = e.
Nous allons définir de deux façons différentes deux transformations de niveaux de gris b et h, où h = b -1, la fonction inverse de b, c.-à-d. y = b(x) ssi x = h(y). Ici b rehaussera les bas niveaux de gris (zones sombres), et inversement h rehaussera les hauts niveaux de gris (zones claires).
1) Soient A et B deux réels > 0 tels que M = A log(1 + MB). Posons:
b(x) = A log(1 + Bx),
h(x) = (ex/A - 1) / B.
Lorsque A diminue, B augmente, et l'effet de rehaussement se renforce.
Le comportement asymptotique de b et h est le suivant:
pour x ~ 0, b(x) ~ AB x et h(x) ~ x / AB;
pour x >> 0, b(x) ~ A log(Bx) et h(x) ~ ex/A / B.
2) Soit n un entier > 0. Posons:
b(x) = M(n-1)/n x1/n,
h(x) = M1-n xn.
Lorsque n augmente, l'effet de rehaussement se renforce.
Dans bien des cas, on peut mesurer les niveaux de gris sur différentes zones de l'image correspondant à certains objets spécifiques, qu'on comparera à des valeurs souhaitables. Par exemple sur une photo d'identité à 256 niveaux de gris, on peut avoir les niveaux de gris suivants :
| Zone | niveau de gris mesuré | niveau de gris souhaitable |
| fond | 105 | 70 |
| cheveux | 120 | 105 |
| chemise | 150 | 190 |
| visage | 180 | 225 |
(NB. Nous avons ordonné ces niveaux de gris du plus sombre au plus clair.)
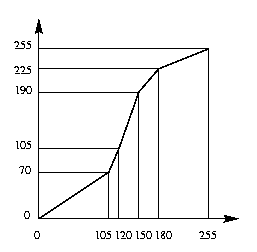
Pour rehausser l'image, on appliquera aux niveaux de gris une transformation f linéaire par morceaux définie par
f(0) = 0,
f(105) = 70,
f(120) = 105,
f(150) = 190,
f(180) = 225,
f(255) = 255,
avec une interpolation linéaire entre les points de contrôle 0, 105, 120, 150, 180, et 255, comme illlustré sur l'image ci-contre.
Plus généralement, pour une image à niveaux de gris compris entre 0 et M, on peut avoir n niveaux de gris
a1, ..., an (tels que 0 < a1 < ... < an < M),
à transformer en n niveaux de gris
b1, ..., bn (où l'on aura le plus souvent 0 < b1 < ... < bn < M),
et on choisira une transformation f linéaire par morceaux donnée par
f(0) = 0, f(a1) = b1, ..., f(an) = bn, et f(M) = M.