Nous allons examiner certaines symétries de l'espace et leur interaction avec les opérations de traitement d'images. On suppose les images définies dans un espace E = Rn ou E = Zn.
Soit P une permutation de E, et soit P-1 l'inverse de P. Ainsi P applique un point p en P(p), et elle transforme une partie X de E en P(X), qui est l'ensemble de tous les points P(x) pour x appartenant à X. Pour une image I à niveaux de gris, la permutation P(I) de I est définie comme suit : si I associe au point q le niveau de gris g, alors P(I) associera ce niveau de gris g au point P(q). Donc :
P(I)(P(q)) = I(q),
d'où en posant p = P(q), on a q = P-1(p) et ainsi
P(I)(p) =I(P-1(p)).
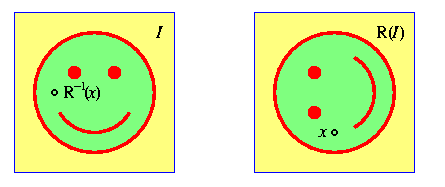
Ceci donne le "principe du mirroir" : pour appliquer une permutation P à une image I, on applique P-1 à l'argument de I. Nous illustrons cette définition ci-dessous pour une rotation R d'un quart de tour dans le sens trigonométrique, appliquée à une image en couleurs :

Dans le cas d'images binaires à valeurs dans {0, 1}, cette définition est compatible avec celle de la permutation d'un ensemble.
Les symétries les plus fondamentales sont les translations. Pour un point p de l'espace, la translation par p, notée Tp, applique l'origine en p et transforme tout point q en Tp(q) = q + p, le translaté de q par p. Le translaté par p d'un ensemble X de points est l'ensemble Tp(X) de tous les Tp(x) = x + p pour x appartenant à X. Pour une image I à niveaux de gris, la translatée Tp(I) de I par p donne :
Tp(I)(q + p) = I(q), et Tp(I)(q) = I(q - p).
L'invariance par translations est une propriété fondamentale partagée par la quasi-totalité des opérations de traitement d'images. Elle exprime le fait qu'une information visuelle sera traitée de la même façon, quelle que soit sa localisation dans l'espace. En effet, si on bouge le capteur, chaque objet sera déplacé dans l'image, mais devra être traité de la même façon que précédemment.
Soit F une opération de transformation d'images. On dit que F est invariante par translations si F commute avec toute translation Tp ; en d'autres termes, pour toute image I et pour tout point p, on a F(Tp(I)) = Tp(F(I)). Cela correspond à l'idée que le traitement d'un objet déplacé donnera le même objet final que pour l'objet en position de départ, sauf que sa position sera déplacée. Nous illustrons ce concept ci-dessous, avec l'opération de boucher les trous puis arrondir les coins :
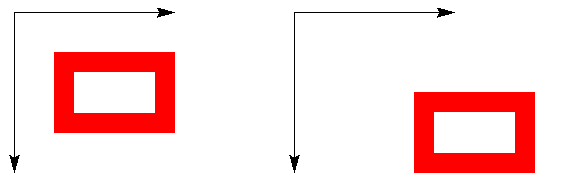
A gauche, une figure X, et à droite sa translation Tp(X).
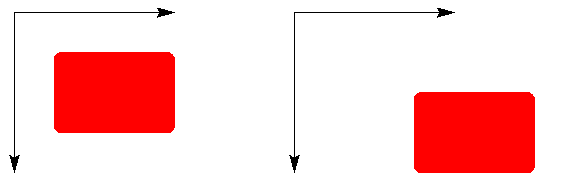
A gauche, F(X), la figure après le traitement ; à droite, F(Tp(X)) = Tp(F(X)), la figure après traitement puis translation, ou translation puis traitement.
De manière générale, toute opération de traitement d'images est supposée invariante par translations, sauf mention contraire explicite. Cela signifie par exemple pour un filtre que la fenêtre autour d'un point aura toujours la même forme et que sa position relative par rapport au point ne changera pas ; pour un filtre linéaire, les coefficients seront placés à la même position relativement au point de référence. Les opérations ponctuelles (transformations des niveaux de gris, par exemple rehaussements) sont trivialement invariantes par translations.