
Outre l'invariance par translation, il convient d'examiner le comportement des opérateurs de traitement d'image par rapport aux autres symétries de l'espace E = Rn ou E = Zn.
Restreignons nous au plan euclidien : E = R2. Une isométrie est une transformation affine préservant les longueurs (elle préservera aussi les angles) ; son déterminant vaut ±1. Une isométrie de déterminant 1 est un déplacement. Tout déplacement est nécessairement une translation ou une rotation ; cette dernière est donnée par un centre c et un angle a, nous l'écrirons Rc,a. La composition d'une rotation et d'une translation donne une rotation de même angle, et toutes les rotations de même angle peuvent être obtenues de cette manière. De plus, la composition de deux rotations de centres quelconques donne une rotation dont l'angle est la somme de leurs deux angles respectifs, sauf quand ces deux angles sont opposés, auquel cas la composition donne une translation (qui sera l'identité quand les deux centres sont identiques). Cela signifie donc que si on prend en compte (pour l'invariance d'un traitement) toutes les rotations de centre et angle arbitraires, il faudra prendre en compte toutes les compositions possibles de celles-ci, c.-à-d. toutes les translations.
Les isométries de déterminant -1 sont les symétries bilatérales et les syméries glissées. Une symétrie bilatérale est donnée par un axe A, nous l'écrirons SA ; une symérie glissée est la composition d'une symétrie bilatérale et d'une translation parallèle à l'axe de la symétrie. La composition de deux symétries bilatérales ou glissées donne un déplacement (rotation ou translation), et tous les déplacements peuvent être obtenus comme composition de deux symétries bilatérales. Cela signifie donc que si on prend en compte (pour l'invariance d'un traitement) toutes les symétries bilatérales, il faudra prendre en compte toutes les compositions possibles de celles-ci, c.-à-d. tous les déplacements.
Par conséquent on considèrera généralement l'invariance d'un traitement par rapport à un des groupes suivants :
Nous avons traité précédemment du cas 1. Nous allons maintenant considérer les cas 2 et 3, et nous terminerons par les cas 4 et 5.
Il existe certaines situations où l'invariance par translations ne s'applique pas. C'est notamment le cas lorsque l'image a une structure circulaire centrée autour d'un point c. Ici on considèrera les rotations de centre c et les symétries bilatérales par rapport à un axe passant par c. On exigera donc d'une opération F de transformation d'images qu'elle soit invariante par rotations de centre c ; cela signifie que F commute avec toute rotation Rc,a de centre c (et d'angle a quelconque), c.-à-d. F(Rc,a(I)) = Rc,a(F(I)) pour toute image I.
On pourra éventuellement postuler en plus l'invariance par symétries bilatérales d'axe A passant par c : F(SA(I)) = SA(F(I)).
Considérons par exemple une image de canopée forestière. Celle-ci est obtenue en plaçant l'appareil photo sur le sol, avec l'objectif dirigé vers le ciel. Une telle image a une structure circulaire centrée autour de son centre (la projection de l'axe vertical).

Image d'une plantation de pin sylvestre à Hartheim, près
de Freiburg i. Breisgau
(de la part de Jean-Michel Noël Walter)
On dit qu'une opération F de transformation d'images est invariante par translations et rotations si F commute avec tout déplacement R (translation ou rotation), c.-à-d. on a F(R(I)) = R(F(I)) pour toute image I. On dit aussi que F est isotrope. Comme tout déplacement est une composition de rotations (de centre et angle variables), il suffit de vérifier que F commute avec toute rotation Rc,a.
L'isotropie signifie qu'une information visuelle sera traitée de la même façon, quelle que soit sa localisation ou son orientation dans l'espace. Ainsi, pour un filtre, la fenêtre autour d'un point sera un disque ou un anneau, et pour un filtre linéaire, les coefficients seront constants sur chaque cercle centré autour du point de référence.
Il est rare de trouver une opération isotrope qui ne soit également invariante par symétries bilatérales ; en d'autres termes, l'opération commutera avec toutes les isométries (de déterminant +1 ou -1).
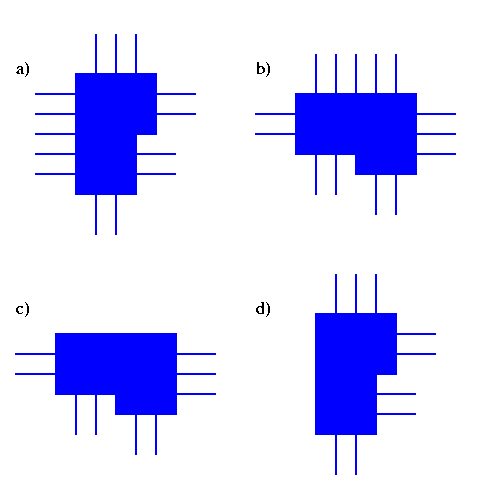
Généralement, une opération invariante par translations n'est pas isotrope. On peut alors considérer ses rotations et symétries. Etant données une isométrie R et une une opération F de traitement d'images, l'application de R à F donne l'opération RFR-1, qui transforme une image I en R(F(R-1(I))). Nous illustrons cette notion pour la rotation R d'un quart de tour dans le sens trigonométrique et l'opération F qui élimine les fines bandes verticales sur le haut d'un objet ; ici RFR-1 éliminera les fines bandes horizontales à gauche de l'objet.
|
|
a) L'image I.
b) On fait une rotation R-1 d'un quart de tour dans le sens trigonométrique inverse : R-1(I). c) On applique l'opération F : F(R-1(I)). d) On fait une rotation R d'un quart de tour dans le sens trigonométrique : R(F(R-1(I))). |
Considérons maintenant le plan discret E = Z2. Les pixels du plan discret sont les points à coordonnées entières. Il faut que les translations, rotations et symétries préservent E.
Pour les translations, on prendra celles par un point à coordonnées entières. Les rotations et symétries préservant l'origine (0,0) forment le groupe des 8 symétries d'un carré (centré à l'origine). Celui-ci comporte 4 rotations (identité, rotations d'un quart de tour à gauche ou à droite, symétrie centrale) et 4 symétries bilatérales (d'axe horizontal, vertical ou diagonal), que nous illustrons ci-dessous.
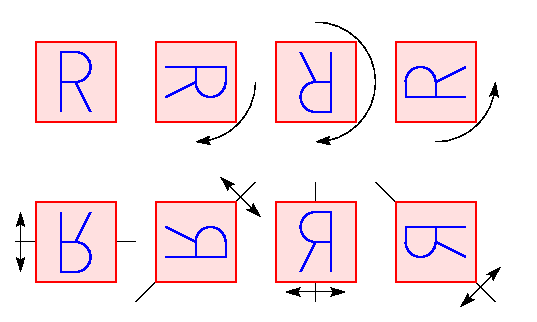
La composition de ces 8 symétries avec les translations donne des rotations de mêmes angles (multiples d'un quart de tour) et des symétries bilatérales ou glissées d'axes parallèles (horizontaux, verticaux ou diagonaux), mais le centre de la rotation pourra avoir ses deux coordonnées entières plus un demi, ou (dans le cas de la symétrie centrale) une seule de ses coordonnées entière plus un demi, tandis que l'axe de la symétrie pourra être translaté d'un entier plus un demi.