d(p,q) +
d(q,r) (inégalité
triangulaire).
Dans le document concernant les chemins, distances et connexités, on a vu deux distances sur le plan discret Z2, la 4-distance d4 et la 8-distance d8 données par :
d4(p,q) = |i-i'| + |j-j'| et d8(p,q) = max( |i-i'| , |j-j'| ) pour p = (i,j) et q = (i',j').
Ce ne sont pas les seules distances possibles, on connaît également la distance euclidienne de donnée par
de(p,q) = sqrt ((i-i')2 + (j-j')2) pour p = (i,j) et q = (i',j').
De façon plus générale, on appelle une distance ou métrique sur le plan discret Z2, toute fonction d définie sur Z2 × Z2 et à valeurs réelles non-négatives, associant à deux pixels p et q la distance d(p,q) de p à q, qui satisfait les trois axiomes suivants :
d(p,q) +
d(q,r) (inégalité
triangulaire).
Ainsi les 4- et 8-distances d4 et d8, de même que la distance euclidienne de sont des métriques. En comparaison avec la distance euclidienne de, la 4-distance est trop longue, tandis que la 8-distance est trop courte. Plus précisément, le long des axes on a d4 = de = d8, tandis qu'en oblique on a d4 > de > d8, et l'écart le plus grand est selon les diagonales, où on a d4 = sqrt(2) de = 2 d8. En d'autres termes, les rapports d4 / de et de / d8 augmentent de 1 à sqrt(2) quand la direction du segment joignant deux points passe d'un axe à une diagonale.
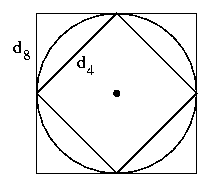
Cela se voit si on dessine pour chacune des distances le cercle de rayon r centré en un pixel p, qui est le lieu des points à distance r de p ; le cercle pour la 4-distance est un losange inscrit dans le cercle euclidien, tandis que celui pour la 8-distance est un carré circonscrit autour du cercle euclidien. C'est le long des diagonales que le losange et le carré s'écartent le plus du cercle ; le losange étant inscrit dans le cercle, cela signifie que la valeur de la 4-distance est supérieure à celle de la distance euclidienne, tandis que le carré étant circonscrit autour du cercle, la valeur de la 8-distance est inférieure à celle de la distance euclidienne.
Dans le cas du maillage cubique, on a des relations des 6- et 26-distances avec la distance euclidienne similaires à celles des 4- et 8-distances, sauf qu'il faut remplacer sqrt(2) et 2 par sqrt(3) et 3 dans les formules vues plus haut.