 dk(p,q) +
dk(q,r)
(inégalité triangulaire).
dk(p,q) +
dk(q,r)
(inégalité triangulaire).
Le plan (ou espace tridimensionnel) discret muni de la relation d'adjacence constitue un graphe, dont les sommets sont les pixels (ou voxels) et les arêtes joignent les paires de pixels adjacents. Les notions de chemin, distance, et connexité dans un graphe prennent ici une forme particulière.
Ecrivons k pour le nombre désignant l'adjacence choisie, c.-à-d. k = 4 ou 8 pour le maillage carré du plan, et k = 6, 18 ou 26 pour le maillage cubique de l'espace tridimensionnel (on peut aussi considérer k = 6 pour le maillage triangulaire du plan). On parlera donc de la relation de k-adjacence entre les pixels (ou voxels).
Un k-chemin du pixel p au pixel q est une suite x0, ..., xn (où n est un entier naturel) de pixels tels que x0 = p, xn = q et pour i = 0, ..., n-1, xi est k-adjacent à xi+1. Ici n est la longueur du chemin. Un chemin de longueur n comporte donc n+1 pixels et n transitions. Par exemple un chemin de longueur 0 comprend un unique pixel, tandis qu'un chemin de longueur 1 est une suite p,q formée de deux pixels k-adjacents.
En maillage carré tout 4-chemin est un 8-chemin, tandis qu'en maillage cubique, tout 6-chemin est un 18-chemin, et tout 18-chemin est un 26-chemin.
La k-distance dk(p,q) entre deux pixels p et q est la longueur minimum d'un k-chemin de p à q. Il s'agit bien d'une distance dans le sens qu'elle vérifie les axiomes suivants :
 dk(p,q) +
dk(q,r)
(inégalité triangulaire).
dk(p,q) +
dk(q,r)
(inégalité triangulaire).
Dans le cas du maillage carré il est facile de voir que si p et q sont de coordonnées (i,j) et (i',j') respectivement, alors
d4(p,q) = |i-i'| + |j-j'| et d8(p,q) = max( |i-i'| , |j-j'| ).
De même, dans le cas du maillage cubique, deux voxels p et q de coordonnées respectives (i,j,k) et (i',j',k') vérifient
d6(p,q) = |i-i'| + |j-j'| + |k-k'| et d26(p,q) = max( |i-i'| , |j-j'| , |k-k'| ).
En comparant ces formules avec celles pour l'adjacence, on voit que deux pixels ou voxels sont k-adjacents (k = 4, 8, 6 ou 26) si et seulement si la k-distance entre eux est 1.
Soit X un ensemble de pixels. On dit que X est k-connexe si pour tous p,q dans X, il existe un k-chemin de p à q entièrement inclus dans X. On vérifie que :
En maillage carré tout 4-chemin est un 8-chemin, donc un ensemble 4-connexe sera toujours 8-connexe. De même en maillage cubique, un ensemble 6-connexe sera toujours 18-connexe, et un ensemble 18-connexe sera toujours 26-connexe.
Un ensemble non vide n'étant pas toujours connexe, on peut alors le décomposer en ses composantes connexes. Soit X un ensemble non-vide de pixels. La relation entre les pixels de X donnée par "il existe un k-chemin de p à q entièrement inclus dans X", est une équivalence. Les classes d'équivalence de celle-ci sont appelées les composantes k-connexes de X. Elles forment une partition de X, c.-à-d. elles sont non-vides, mutuellement disjointes, et recouvrent X. Donc pour tout pixel p de X, la composante connexe de X contenant p est formée de tous les pixels q de X tels qu'il existe un k-chemin de p à q entièrement inclus dans X ; c'est aussi la réunion de toutes les parties k-connexes de X contenant p. En fait, une partie Y de X est une composante k-connexe de X si et seulement si Y est une partie k-connexe maximale de X.
En maillage carré une composante 8-connexe de X est la réunion d'une ou plusieurs composantes 4-connexes de X reliées entre elles par des connexions en diagonale. C'est ce que nous illustrons ci-dessous :
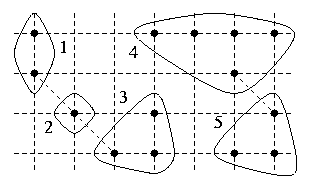
Dans cet exemple, les composantes 4-connexes sont les ensembles numérotés de 1 à 5, tandis que les composantes 8-connexes sont d'une part la réunion des ensembles 1 à 3, d'autre part la réunion des ensembles 4 et 5.
De même en maillage cubique, une composante 26-connexe est la réunion d'une ou plusieurs composantes 18-connexes, une composante 18-connexe est la réunion d'une ou plusieurs composantes 6-connexes.