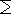 q
q
 E
F(q)G(p - q) ,
E
F(q)G(p - q) ,
La classe la plus connue de filtres spatiaux est celle qui se base sur le principe de superposition linéaire. On considère des images à niveaux de gris sur un espace E de points, avec des niveaux de gris dans R, comme des fonctions définies sur E et à valeurs dans R. Une combinaison linéaire de deux images I1 et I2 par des coefficients scalaires a1 et a2 est l'image a1I1 + a2I2, dont le niveau de gris en chaque point p est la combinaison linéaire des niveaux de gris des deux images respectives :
[a1I1 + a2I2](p) = a1I1(p) + a2I2(p) .
Un opérateur F de traitement d'images transforme une image I en une image F(I). On dit que cet opérateur F est linéaire si son fonctionnement satisfait le principe de superposition linéaire, à savoir
F(a1I1 + a2I2) = F(a1I1) + F(a2I2)
pour deux images I1 et I2 et deux scalaires a1 et a2 quelconques. Intuitivement, cela signifie que si on traite un fondu entre deux images, cela revient au même que de traiter les deux images séparément, et de faire un fondu des deux images résultantes. Sans information supplémentaire, une telle opération dépend d'un grand nombre de paramètres. Par exemple, si l'espace E est constitué de n pixels, l'opérateur F sera décrit par une matrice n × n. On suppose donc que E = Rn ou E = Zn, et que F est invariant par translations, c.-à-d. pour tout point p de E, F commute avec Tp, la translation par p :
F(Tp(I)) = Tp(F(I))
pour toute image I. On appellera généralement un filtre linéaire un opérateur obéissant aux deux principes de superposition linéaire et d'invariance par translations. En pratique, surtout pour les images numériques, on postule un troisième principe, celui de localité : à tout point p de E, on associe une fenêtre bornée W(p) (indépendante de l'image I), et la valeur de F(I)(p) ne dépend que des valeurs I(q) pour les points q dans W(p) ; en d'autres termes, F(I)(p) = F(I|W(p))(p), où I|W(p) est l'image ayant les mêmes valeurs que I dans W(p), et valant 0 partout ailleurs.
Etant données deux images F et G sur E = Zn, la convolution de F et G est l'image F * G définie par
(F * G)(p) =
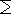 q
q
 E
F(q)G(p - q) ,
E
F(q)G(p - q) ,
où on suppose que la série converge absolument. On définit supp(F), le support de F, comme l'ensemble des points p où la valeur F(p) est non-nulle. Alors
(F * G)(p) =
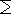 q
q
 supp(F)
F(q)G(p - q) .
supp(F)
F(q)G(p - q) .
Ainsi, lorsque F est à support fini, la série est en fait une somme finie, il n'y a donc aucun problème de convergence. Dans le cas où E = Rn, dans la définition il faut remplacer la somme sur q par l'intégrale sur E selon dq.
La convolution est bilinéaire :
[a1F1 +
a2F2] * G
= a1(F1 * G) +
a2(F2 * G) ,
F *
[a1G1 +
a2G2] =
a1(F * G1) +
a2(F * G2) ,
commutative et associative :
F * G = G * F ,
(F * G) * H =
F * (G * H) ,
et elle commute avec les translations :
Tp(F * G) = Tp(F) * G = F * Tp(G) .
Grâce à la bilinéarité et à la commutation avec les translations, pour une image fixée M, l'opérateur transformant une image I en la convolution M * I est un filtre linéaire (il satisfait les deux principes de superposition linéaire et d'invariances par translation). On appelle parfois M le masque de convolution. Typiquement, ce sera une image à support borné.
Le filtre I -> M * I détermine de façon unique le masque M. En effet, on définit une impulsion sur E = Zn comme étant l'image i telle que i(p) = 1 pour p = 0 (l'origine), et = 0 sinon ; pour E = Rn, l'impulsion sera la distribution "delta de Dirac". Alors la convolution du masque par l'impulsion donne le masque lui-même :
M * i = M .
Aussi on appelle le masque M la réponse impulsionnelle du filtre I -> M * I. Pour E = Zn, on peut facilement montrer que tout filtre linéaire F satisfaisant le principe de localité est donné par la convolution avec un masque M de support borné, qui est en fait la réponse impulsionnelle de F :
F(I) = M * I , où M = F(i) .
Pour E = Rn, cela reste vrai si on suppose que F satisfait certaines conditions de "continuité".
On considère un masque de convolution M de support S borné ; donc on peut considérer M comme une fonction définie sur S et à valeurs dans R. D'après la formule de convolution, pour calculer (M * I)(p) en un point p de E, pour chaque point q de S, il faut multiplier M(q) par I(p - q), et ensuite additionner les résultats. Visuellement parlant, on procède comme suit :
Nous illustrons cela ci-dessous avec un masque de support 3 × 3 centré sur l'origine :
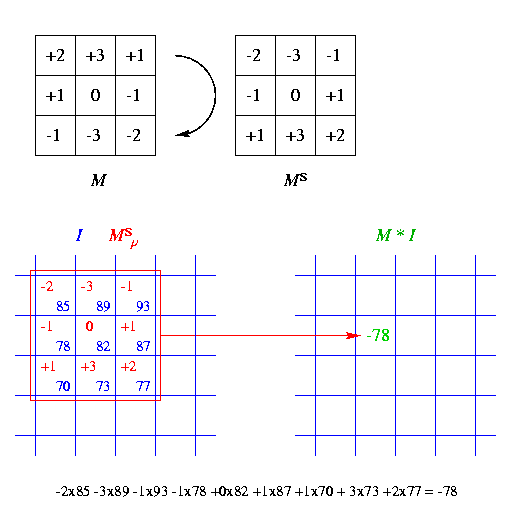
Une variante de la convolution est la corrélation, définie comme suit : la corrélation de F et G est l'image F o G définie par
| (F o G)(p) | = 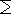 q q
 E
F(q)G(p + q) , E
F(q)G(p + q) ,
|
= 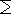 q q
 supp(F)
F(q)G(p + q) . supp(F)
F(q)G(p + q) .
|
On notera que F o G = Fs * G, où Fs est l'image "retournée" par symétrie centrale : Fs(p) = F(-p). Le mode opératoire est le même que pour la convolution, sauf qu'il ne faut pas appliquer la symétrie centrale au masque F. Dans la plupart des cas, on utilise un masque de convolution M symétrique (M(-p) = M(p)) ou antisymétrique (M(-p) = -M(p)), donc la convolution et la corrélation donnent la même chose, à un signe près dans le cas antisymétrique.
Un intérêt particulier de la corrélation est
qu'elle permet de mesurer si deux images F et G sont
assez semblable à une translation près. On mesure la
valeur absolue de |(F o
G)(p)| pour tous les points p de
E, et là où cette valeur atteint un pic, cela
signifie les valeurs F(q) et G(p +
q) sont bien corrélées, par exemple F
est à peu près un multiple de la translatée de
G par p.