Pour divers types d'images il existe une opération N transformant une image I en son "négatif" N(I). On suppose que "le négatif du négatif est l'image originelle", c.-à-d. N(N(I))= I, en d'autres termes l'opération N est sa propre inverse. En fonction du type d'image, ce négatif peut se définir de façon naturelle :
Une telle opération N intervertissant figure et fond, clair et sombre, et vérifiant N(N(I))= I, s'appelle une inversion.
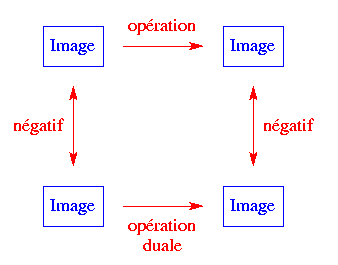
Le dual par inversion d'une opération de traitement d'images est la transformation qui sera effectuée sur le négatif tandis que l'opération sera appliquée à l'image. On a le diagramme suivant :

Donc pour une opération F de traitement d'images, son dual F* est l'opération vérifiant F*(I) = N(F(N(I))) pour une image I. Par exemple, pour les ensembles, le dual d'un opérateur arrondissant les coins convexes d'une figure, arrondira les coins concaves d'une figure (cfr. ci-dessous, avec la figure en bleu et le fond en jaune).
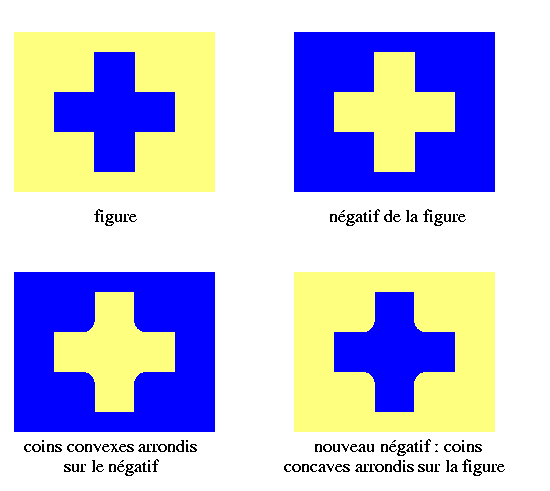
Par ailleurs, le dual d'un opérateur éliminant les petites composantes connexes de la figure, éliminera les petites composantes connexes du fond.
Pour les images à niveaux de gris, comme le négatif intervertit les zones claires et sombres d'une image, le comportement du dual F* sur les zones claires sera celui de l'opérateur initial F sur les zones sombres, et vice versa.
Comme N(N(I))= I, on a F** = F, le dual du dual est l'opérateur initial.
Un opérateur qui est son propre dual (F* = F) est appelé auto-dual. Il se comportera donc de la même façon sur la figure et le fond (pour les ensembles), ou sur les zones claires et sombres (pour les images à niveaux de gris).