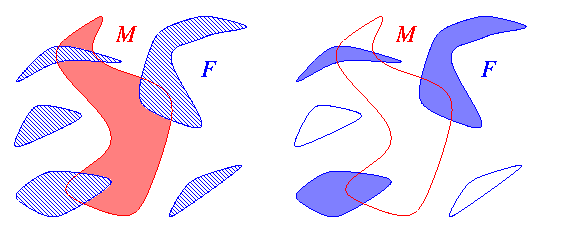
A gauche, le marqueur M en rouge, et les composantes connexes de la figure F hachurées en bleu.
A droite, en bleu plein les composantes connexes de F intersectant M ; elles seront reconstruites.
Il est des situations où un algorithme se base sur une propagation d'informations selon des chemins qui ne suivent pas le sens de balayage. Dans ce cas on utilisera une file (de type FIFO : premier entré, premier sorti), et la propagation se fera alors d'un pixel extrait de la file vers ses voisins qui seront ensuite insérés dans la file.
On suppose que les images sont définies sur un domaine discret D, et qu'à chaque pixel p de D on associe une fenêtre W(p) incluse dans D. On a une fonction f qui, à partir de deux pixels p et q, où q est dans W(p), et de leurs valeurs I(p) et I(q) dans une image I, calcule la nouvelle valeur pour I(q), qui sera récrite dans l'image I. C'est à travers la modification des valeurs de I que se fera la propagation d'information.
Soit I une image définie sur D, et M un sous-ensemble de D, appelé marqueur, à partir duquel démarrera la propagation. L'algorithme prend la forme suivante :
Comme dans l'algorithme séquentiel, la nouvelle valeur I(q) calculée en un pixel q est récrite directement dans l'image de départ, et ainsi cette valeur peut dépendre de toutes les valeurs calculées sur les pixels précédemment extraits de la file. A la différence de l'algorithme séquentiel, l'ordre de propagation ne sera plus celui de balayage. Mais il y a un autre aspect qui oppose d'une part cet algorithme, d'autre part les algorithmes parallèles et séquentiels. Dans l'algorithme à base de file, la valeur I(p) du pixel courant p est utilisée pour modifier la valeur I(q) des pixels q de la fenêtre W(p) ; en d'autres termes, le pixel courant exporte l'information vers ses voisins. Dans les algorithmes parallèles et séquentiels, la valeur I(p) du pixel courant p est modifiée en fonction de la valeur I(q) des pixels q de la fenêtre W(p) ; en d'autres termes, le pixel courant importe l'information depuis ses voisins.
Un exemple typique d'utilisation d'algorithme à base de file est la reconstruction dans une figure, de toutes les composantes connexes intersectant un marqueur. Nous l'illustrons ci-dessous :
A gauche, le marqueur M en rouge, et les composantes
connexes de la figure F hachurées en bleu.
A
droite, en bleu plein les composantes connexes de F
intersectant M ; elles seront reconstruites.
Ici les valeurs associées aux pixels dans l'image seront 0 pour les pixels du fond, 1 pour les pixels de la figure qui ne sont pas (ou pas encore) dans la reconstruction, et une troisième valeur e (par exemple 2) pour les pixels de la figure qui sont dans la reconstruction. L'algorithme à base de file prend alors la forme suivante :
Ainsi énoncé, cet algorithme permet la reconstruction de
composantes connexes dans n'importe quel graphe (il est d'ailleurs une
variante de l'algorithme classique de parcours en
largeur). Dans le cas des figures dans
Z2, on peut mieux exploiter la structure
topologique de cet espace. Au lieu de considérer les pixels de
la figure, on peut prendre les segments horizontaux de
celle-ci. Un segment horizontal de la figure, codé sous la
forme [i,a,b] (avec a
b), est un ensemble
contigu {(i,a), ...,
(i,b)} de pixels sur une ligne,
appartenant tous à la figure, mais dont les voisins gauche
(i,a-1) et droit(i,b+1)
appartiennent au fond.
Dans l'algorithme ci-dessus, on peut remplacer partout "pixel" par "segment". En pratique, cela est possible si on code la figure comme un ensemble de segments, avec une structure de données qui permet à partir d'un segment d'accéder immédiatement aux segments qui lui sont adjacents. Mais le plus simple est de construire les segments au fur et à mesure qu'on reconstruit les composantes connexes intersectant le marqueur :
Sous cette forme, l'algorithme est très semblable à celui dit de seed fill (remplissage à partie de graine) utilisé en infographie pour remplir ou colorer une zone à partir d'un pixel appelé graine.
De même que l'algorithme de parcours en largeur dans un graphe donne le plus court chemin de chaque sommet vers un sommet choisi comme racine, un algorithme à base de file permet de donner le plus court 4- ou 8-chemin, contraint à l'intérieur d'un masque, de tout pixel vers le plus proche pixel appartenant à un marqueur donné.
Soit S une partie connexe de Z2, pas nécessairement convexe, appelée masque ou domaine. On considère les 4- ou 8-chemins entre pixels de S, entièrement inclus dans S ; un tel chemin est dit géodésique, et la longueur minimum d'un 4-/8-chemin géodésique entre deux pixels p et q de S est la 4-/8-distance géodésique entre p et q. Nous illustrons cela ci-dessous :
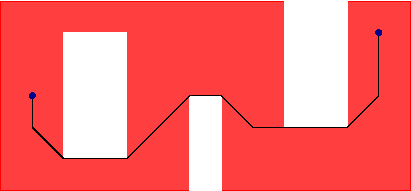
Le plus court 8-chemin géodésique entre deux
pixels, dans un masque non convexe ayant un trou.
Soit R une partie de S, appelée marqueur. La transformée de distance géodésique de R dans S est la fonction qui associe à tout pixel p de S la distance géodésique minimum de p à un pixel de R. Posons :
S, f(p) sera la
k-distance géodésique de p à
R.
S le pixel suivant dans le plus court k-chemin
géodésique de p à R ; si
p R, il n'y a pas
de pixel suivant, et on donne la valeur "NIL" à
s(p).
L'algorithme à base de file prend alors la forme suivante :
S,
R, on
pose f(p) := 0 et s(p) := NIL, et
on insère p dans la file ;
S\R, on
pose f(p) := H.
Vk(p), si f(q)
= H, alors on pose f(q) := f(p) +
1 et s(q) := p, et on insère
q dans la file.
On remarquera que les pixels sont insérés dans la file dans l'ordre de leur distance géodésique au marqueur. Tout pixel est inséré une seule fois dans la file, et à ce moment-là, il reçoit la valeur exacte de sa distance géodésique au marqueur.
Par contre, si au lieu de considérer la 4- ou la 8-distance, on utilise une distance de chanfrein (correspondant à un graphe d'adjacence pondéré sur les pixels), cet algorithme ne fonctionne pas correctement, parce que l'ordre d'insertion des pixels dans la file correspond à la distance au marqueur dans le graphe non pondéré, tandis que la distance de chanfrein se base sur le graphe pondéré. Si on écrit V(p) pour le voisinage de p sur lequel est défini le masque de chanfrein, et Mp pour le masque de chanfrein en p, alors le point 2.ii ci-dessus prendra la forme :
Pour chaque pixel q
alors on pose f(q) := f(p) + Mp(q) et s(q) := p, et on insère q dans la file.
Ainsi écrit, l'algorithme donnera un résultat final correct, mais il ne sera pas optimal. En effet, un pixel pourra être inséré plusieurs fois dans la file ; à chaque insertion, la valeur f(q) estimant sa distance géodésique au marqueur sera diminuée, et certains de ses voisins seront insérés à nouveau dans la file. C'est ce que nous illustrons ci-dessous pour la distance (5,7,11) :
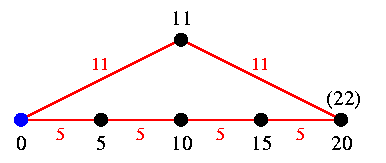
En rouge, les distances données par le masque de
chanfrein.
Le pixel bleu à gauche forme le marqueur.
Le
pixel à droite est à distance 20 de celui-ci, mais avant
de recevoir cette valeur,
il recevra la valeur 22 du pixel à
distance 11 de lui-même et du marqueur.
La solution à ce problème sera décrite dans le document suivant : on utilisera un ensemble de files ordonné selon la valeur de f(p) (aussi appelé file hiérarchique), et on attachera à chaque pixel un booléen indiquant s'il a déjà été traité par l'algorithme.