L'équivalent tridimensionnel d'un pixel est appelé voxel. Comme pour le plan, on peut représenter la subdivision de l'espace en voxels par un pavage. Le seul polyèdre régulier permettant un pavage est le cube. Il est donc d'usage, pour les images tridimensionnelles, d'utiliser un pavage cubique, auquel correspond un maillage cubique. Ce maillage forme un réseau, donc les voxels, identifiés aux points du maillage, correspondent aux points de l'espace ayant leurs 3 coordonnées entières et l'ensemble des voxels est identifié à Z3.
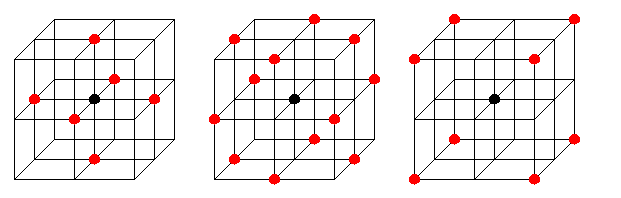
Un voxel a 26 voisins, se répartissant en trois types :
En fait ces trois types de voisins ont leurs coordonnées qui diffèrent de 1 selon respectivement 1, 2 ou 3 coordonnées (et identiques selon les 2, 1 ou 0 coordonnées restantes). Nous illustrons ci-dessous ces trois types de voisins dans le maillage :

Comme dans le cas du plan, on regroupe chaque type de voisin avec les types prédents: 6 voisins axiaux, 6 + 12 = 18 voisins axiaux ou diagonaux, 6 + 12 + 8 voisins axiaux, diagonaux ou diamétraux. On définit ainsi trois relations d'adjacence sur les voxels ; deux voxels (i,j,k) et (i',j',k') sont dits :
 2
et max( |i-i'| ,
|j-j'| , |k-k'| ) = 1.
2
et max( |i-i'| ,
|j-j'| , |k-k'| ) = 1.
On voit que les 6- et 26-adjacences pour les voxels sont les analogues des 4- et 8-adjacences pour les pixels.
Il existe des pavages avec des polyèdres non réguliers, ceux-ci sont parfois étudiés en vue de donner des propriétés semblables à celles du pavage hexagonal dans le plan (par exemple que deux pavés d'intersection non vide se touchent par une face).
A n dimensions, on a un pavage et un maillage hypercubique. On a alors n relations d'adjacence entre hypervoxels (selon le nombre maximum de coordonnées différant de 1). Les extrèmes sont, pour deux hypervoxels (x1, ..., xn) et (y1, ..., yn) :
Ce sont les analogues des 4- et 8-adjacences pour les pixels.