
Une abstraction mathématique des pixels comme taches lumineuses consiste à considérer qu'ils forment des ensembles connexes de points du plan euclidien, de telle sorte que deux pixels voisins ne peuvent s'intersecter que sur leur bord, et que l'ensemble des pixels recouvre le plan. Une telle décomposition du plan s'appelle un pavage.
Il n'y a que 3 types de pavages dont les pavés sont des polygones réguliers : triangulaire, carré, et hexagonal. Nous les illustrons ci-dessous :

On place un point au centre de chaque pavé, et on joint par une ligne ceux parmi ces points dont les pavés correspondants se touchent par un côté. Cela donne le maillage correspondant au pavage, comme illustré ci-dessous :
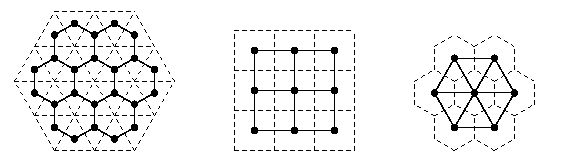
Comme on peut le voir, le pavage carré donne un maillage carré, tandis que le pavage triangulaire donne un maillage hexagonal et vice versa. C'est ce qu'on appelle la dualité entre pavages et maillages.
Les centres des pavés seront les points discrets correspondant aux pixels. Pour les pavages carré et hexagonal, ces points forment un réseau, c.-à-d. ils coïncident avec les points à coordonnées entières selon deux axes ; ces axes sont orthogonaux pour le pavage carré, et forment un angle de 60° ou de 120° pour le pavage hexagonal, comme on le voit ci-dessous :
Cela représente un avantage indéniable des pavages hexagonal et carré par rapport au triangulaire. Ce dernier a un autre défaut : chaque pavé a 12 pavés voisins se répartissant en trois types différents, à savoir 3 pavés le touchant par un côté, 3 le touchant par un sommet et en symétrie par rapport à ce sommet, et enfin 6 le touchant par un sommet et formant avec ce pavé un angle de 120° par rapport à ce sommet. Par conséquent, on n'utilise jamais le pavage triangulaire comme modèle de pixels.

Dans le pavage carré, chaque pavé a 8 pavés voisins se répartissant en deux types, à savoir 4 pavés le touchant par un côté et 4 le touchant par un sommet. En d'autres termes, dans le maillage carré, chaque point a 8 voisins, 4 selon les axes et 4 selon les diagonales. Par contre dans le pavage hexagonal, chaque pavé a 6 pavés voisins tous du même type, qui sont les 6 pavés le touchant par un côté. Donc dans le maillage triangulaire correspondant au pavage hexagonal, chaque point a 6 voisins, tous du même type.
Par conséquent le pavage hexagonal a la topologie la plus simple du point de vue mathématique et algorithmique (6 voisins au lieu de 8, et d'un seul type au lieu de deux). De plus, il se prête mieux à la modélisation de phénomènes naturels. Par exemple sur un réseau triangulaire, la modélisation discrète de la dynamique des molécules d'un fluide (liquide, gaz) permet de retrouver à l'échelle macroscopique les lois de la physique des fluides ; ce n'est pas le cas si on prend un maillage carré.
Cependant, on utilise presque toujours le pavage et le maillage carrés, car ils correspondent à nos habitudes cartésiennes. En particulier les points lumineux d'un écran sont toujours disposés suivant un maillage carré.
Un point du maillage sera appelé pixel. Comme le maillage forme un réseau, les pixels sont les points à coordonnées entières selon deux axes. Donc tout pixel se code comme un couple (i,j) d'entiers, et l'ensemble des pixels correspond à Z2. En maillage carré il est d'usage de prendre le premier axe i orienté vers le bas et le deuxième axe j orienté vers la droite ; ainsi les coordonnés correspondent à la notation matricielle, le pixel (i,j) se trouvant à l'intersection de la ligne i et de la colonne j.
Dans un maillage carré (aussi appelé grille), tout pixel a 2 types de voisins, à savoir ses 4 voisins selon les axes, et ses 4 voisins selon les diagonales. La relation de proximité entre deux voisins axiaux est plus forte que celle entre deux voisins diagonaux. Par conséquent nous définissons deux relations d'adjacence sur les pixels de ce maillage : deux pixels p et q sont dits
Les nombres 4 et 8 correspondent au nombre de pixels adjacents à un pixel donné pour le type d'adjacence choisi. Pour le maillage triangulaire (correspondant au pavage hexagonal), il n'y a qu'une seule relation d'adjacence, appelée 6-adjacence. Les 3 relations d'adjacence sont illustrées ci-dessous :
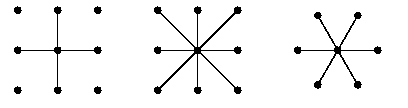
Etant donné un pixel (i,j), en maillage carré les pixels adjacents à (i,j) sont :
On vérifie les relations suivantes :
En maillage triangulaire, les pixels 6-adjacents à (i,j) sont (cfr. l'illustration du réseau plus haut) :