 |
 |
 |
||
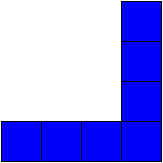
| Figure de départ | Après balayage de la première ligne |
Après balayage de la dernière ligne |
La réduction homotopique consiste à enlever successivement des pixels d'une figure, de telle manière que la topologie ne change pas tout au long du processus. On parle de squelettisation homotopique quand cette réduction doit aboutir à un squelette ayant non seulement la même topologie, mais aussi la même forme générale que la figure.
La topologie dépend du choix de la connexité sur la figure et sur le fond (4- sur l'un, 8- sur l'autre). En fait, la majorité des algorithmes de squelettisation considère la 8-connexité sur la figure et la 4- sur le fond, ce qui a l'avantage de garder moins de pixels dans le squelette ; en effet, une ligne diagonale requiert 2 fois moins de pixels en 8-connexité qu'en 4-connexité.
Cette réduction s'opère par la répétition d'une procédure d'amincissement, qui examine les pixels du bord de la figure, et enlève ceux qui vérifient un critère :
Algorithme : Réduction
Répéter
Amincissement
jusqu'à ce que la figure ne change plus.
La succession des étapes d'amincissement est en quelque sorte l'analogue de la suite des instants dans le processus de feu de prairie. Suivant que cet amincissement traite les pixels de la figure séquentiellement ou en parallèle, on dira que l'algorithme de réduction (ou squelettisation) est séquentiel ou parallèle.
La procédure d'amincissement est séquentielle, ce qui signifie que les pixels sont examinés selon un ordre de balayage, et que chaque fois qu'un pixel change de valeur (de 1 pour la figure à 0 pour le fond), la nouvelle valeur est écrite dans la figure. Ceci implique que lors de l'examen d'un pixel, tous les pixels précédemment balayés ont leur nouvelle valeur, et tous ceux pas encore balayés ont l'ancienne. La décision concernant un pixel est prise en fonction de la configuration de pixels dans un voisinage de celui-ci (généralement 3 × 3), pour lequel on vérifie si un certain critère d'enlevabilité du pixel est vérifié. La procédure d'amincissement prend donc la forme (où I est l'image binaire codant la figure) :
Procédure : Amincissement séquentiel
Pour le pixel p allant du premier au dernier, faire
si I(p) = 1 (p est dans la figure) et si le voisinage de p satisfait le critère,
alors I(p) := 0 (p est enlevé de la figure et rajouté au fond).
Pour que cette réduction soit homotopique, la condition nécessaire et suffisante est que tout pixel dont le voisinage satisfait le critère doit être simple. D'ailleurs, pour une réduction ultime (qui enlève le plus de pixels possibles, sans tenir compte de la forme de la figure), le critère sera effectivement "le pixel est simple", ce qui peut se vérifier par la configuration de pixels de la figure et du fond dans le voisinage 3 × 3 de celui-ci.
Si l'homotopie est facilement vérifiable pour un amincissement séquentiel, le problème de cette approche est que l'ordre de balayage induit un biais sur la forme et le positionnement de la figure réduite. C'est ce que nous illustrons ci-dessous pour une réduction :
 |
 |
 |
||
| Figure de départ | Après balayage de la première ligne |
Après balayage de la dernière ligne |
Une solution possible est de ne pas balayer la figure dans l'ordre lexicographique, mais :
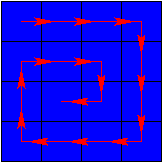
Nous illustrons ci-dessous ce que cela donne pour l'exemple plus haut :
 |
 |
|
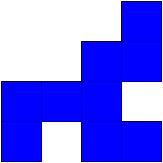
| Ordre de balayage | Réduction obtenue |
Il reste encore un léger biais suivant l'ordre de balayage de chaque classe de pixels équidistants du fond.
Le biais sur la forme de la figure réduite induit par l'ordre de balayage, a conduit de nombreux auteurs à élaborer des algorithmes basés sur un amincissement parallèle. Ici tous les pixels sont examinés indépendamment les uns des autres, et leurs valeurs sont copiées dans une nouvelle image. La procédure d'amincissement prend donc la forme suivante (où I et J sont les deux images binaires codant la figure avant et après amincissement) :
Procédure : Amincissement parallèle
Pour chaque pixel p, faire
si I(p) = 1 (p est dans la figure) et si le voisinage de p satisfait le critère,
alors J(p) := 0 (p est enlevé de la figure et rajouté au fond),
sinon J(p) := I(p) (le pixel n'est pas modifié).
I := J.
NB. En pratique, I := J ne signifie pas qu'on recopie le tableau J dans le tableau I, mais plutôt qu'on intervertira les pointeurs sur les deux tableaux.
Le problème avec cette approche est que la préservation de la topologie est plus difficile à garantir. En effet, on peut avoir un groupe de pixels qui sont chacun individuellement simple, mais tels qu'en les enlevant tous ensemble, la topologie de la figure n'est pas préservée. C'est ce que nous illustrons dans l'exemple ci-dessous:
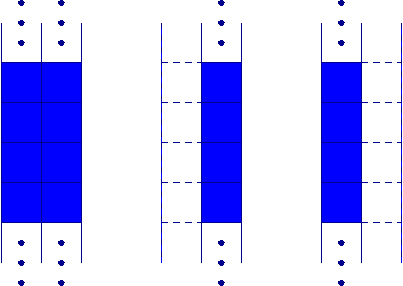
Dans une bande verticale de largeur 2, chaque pixel est
simple.
On peut, sans modifier la topologie, enlever soit la
rangée
de gauche, soit celle de droite, mais pas les deux
à la fois.
La non-préservation de la topologie est l'erreur la plus fréquente dans l'élaboration d'un algorithme parallèle de réduction. Il y a principalement 3 approches pour une réduction ou squelettisation parallèle préservant la topologie, les deux premières sont basées sur une décomposition de l'amincissement, tandis que la troisième utilise en chaque pixel une information plus forte que la configuration de son voisinage 3 × 3 :
Elle consiste à décomposer l'étape d'amincissement en plusieurs sous-étapes amincissant les bords haut, gauche, bas et droit de la figure. Elle remonte aux travaux de Rosenfeld en 1970. Appelons N (nord), W (ouest), S (sud) ou E (est) un pixel de la figure, selon que son 4-voisin du côté respectivement N, W, S ou E, appartient au fond. Formellement :
Ainsi dans l'exemple de la bande verticale ci-dessus, les pixels de la rangée gauche sont W, et ceux de la rangée droite sont E. Si on n'enlève pas simultanément les pixels W et E, la bande ne sera pas effacée. Ceci suggère donc de décomposer l'amincissement en 4 sous-étapes N, W, S et E :
Procédure : Amincissement parallèle 4-directionnel
- amincissement parallèle des pixels N selon le critère N.
- amincissement parallèle des pixels W selon le critère W.
- amincissement parallèle des pixels S selon le critère S.
- amincissement parallèle des pixels E selon le critère E.
En fait l'ordre des 4 sous-étapes N, W, S et E n'est pas important. Ainsi dans l'exemple ci-dessus de la bande large de deux pixels, la rangée de gauche sera enlevée si l'amincissement W a lieu avant l'E, sinon ce sera la rangée de droite qui sera enlevée.
Il est possible de combiner l'amincissement N avec un des deux amincissements W et E, et de combiner le S avec l'autre. En effet, l'important est de ne pas enlever simultanément les pixels N et S (ou W et E). Cela donne la variante ci-dessous :
Procédure : Amincissement parallèle 2-directionnel
- amincissement parallèle des pixels N ou W selon le critère NW.
- amincissement parallèle des pixels S ou E selon le critère SE.
A nouveau le choix des combinaisons (soit NW et SE, soit NE et SW), et l'ordre des deux sous-étapes, ne sont pas importants.
En ce qui concerne la préservation de la topologie et de la
forme de la figure, Rosenfeld montra qu'une opération qui
enlève en parallèle tous les pixels N de la figure
vérifiant un certain critère concernant le
voisinage,
préserve la topologie pour la 8-connexité sur la figure et la 4- sur le fond, et
ne réduit pas un 8-chemin "simple" (où tous les pixels sont mutuellement distincts, et deux pixels non successifs ne sont pas 8-adjacents),
si et seulement si
tout pixel satisfaisant le critère est simple et 8-adjacent à au moins deux pixels de la figure.
L'idée ici est de décomposer la figure, non pas selon l'orientation du bord, mais selon la parité des pixels. Appelons un pixel pair ou impair selon que la somme de ses coordonnées est paire ou impaire. La partition du plan Z2 en pixels pairs et impairs correspond à la répartition des cases blanches et noires du damier ; en fait, deux pixels 4-adjacents sont de parités opposées, tandis que deux pixels diagonalement adjacents sont de même parité. Les deux ensembles de pixels respectivement pairs et impairs sont appelés sous-mailles. On va enlever de la figure alternativement les pixels pairs et les impairs, en utilisant dans les deux cas le même critère, d'où :
Procédure : Amincissement parallèle à 2 sous-mailles
- amincissement parallèle des pixels pairs.
- amincissement parallèle des pixels impairs.
A nouveau, l'ordre entre pair et impair n'importe pas. Nous illustrons ci-dessous ce que cela donne dans l'exemple ci-dessus de la bande de largeur 2.
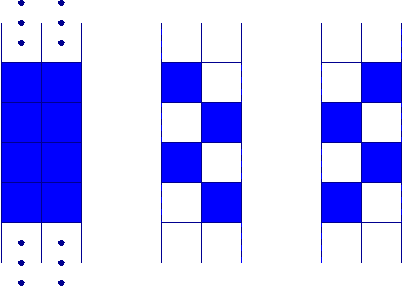
La bande verticale de largeur 2, et les deux réductions
obtenues selon qu'on y enlève les pixels pairs ou impairs.
Notons d'abord que la réduction obtenue est un ensemble 8-connexe et non 4-connexe. En fait, l'approche par les 2 sous-mailles paire/impaire ne fonctionne que pour le choix de la 8-connexité sur la figure et la 4- sur le fond. On remarquera ensuite que la bande de largeur 2 est devenue un zig-zag, qui représente en quelque sorte un compromis entre le positionnement à gauche ou à droite de la réduction. D'ailleurs on reconnaît facilement les algorithmes de squelettisation à base de sous-mailles, à ce qu'ils transforment une bande de largeur paire en une ligne en zig-zag le long des deux rangées au centre de la bande.
Ici on ne décompose pas la figure, on utilise le même citère pour tous les pixels, et tous ceux qui le satisfont sont enlevés de la figure. On peut voir que pour éviter le problème vu plus haut, la configuration de pixels de la figure et du fond dans le voisinage 3 × 3 centré sur un pixel ne suffit pas à déterminer si on peut l'enlever.
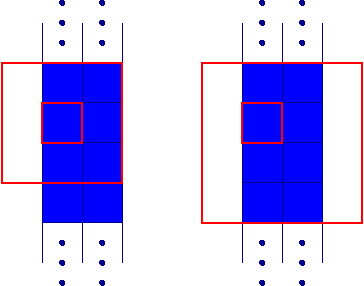
Le voisinage 3 × 3 centré sur un pixel de la bande
de
gauche "ne voit pas" que la bande de droite est au
bord de
la figure. Un voisinage plus grand donne cette
information.
On peut donc utiliser soit un voisinage 4 × 4 (nécessairement non centré, ce qui implique que le critère pour enlever un pixel ne sera pas isotrope) ou 5 × 5, soit un voisinage 3 × 3 en y intégrant d'autres informations que l'appartenance de chaque pixel à la figure ou au fond, par exemple lesquels parmi les pixels du voisinage sont simples (notons que cette information est donnée si on a le voisinage 3 × 3 de chaque pixel du voisinage 3 × 3, en d'autres termes le voisinage 5 × 5 du pixel examiné).
De tels algorithmes de réduction sont dits fortement parallèles. Leur conception est très difficile. Notons ceux de Manzanera (à 2, 3, voire n dimensions), dont il a été prouvé qu'ils préservent la topologie.
On voudrait pouvoir combiner les avantages d'un algorithme séquentiel (facilité de la préservation de la topologie) et d'un parallèle (absence de biais induit par l'ordre de balayage, d'où un squelette mieux centré). Pour cela on peut utiliser un algorithme séquentiel à mémoire. Les pixels sont traités dans l'ordre de balayage, comme pour un algorithme séquentiel ; quand on décide de modifier la valeur d'un pixel, on retient alors la double information de sa valeur initiale et de sa nouvelle valeur. Ainsi pour tous les pixels antérieurs (dans l'ordre de balayage) à un pixel donné, l'information de leur valeur initiale correspond au fonctionnement d'un algorithme parallèle, et celle de leur nouvelle valeur correspond à celui d'un algorithme séquentiel.
Ici le seul changement de valeur possible est de 1 (appartenant à la figure) vers 0 (appartenant au fond). On prendra donc une troisième valeur, par exemple 2, pour coder un pixel qui dans l'étape d'amincissement passe de la figure au fond. Le critère appliqué à un pixel, qui se base sur un examen de la configuration de valeurs dans le voisinage de ce pixel, devra se comporter comme pour un algorithme séquentiel du point de vue de la topologie, mais comme un algorithme parallèle du point de vue de la géométrie. La différence entre les deux tient aux pixels marqués 2 (à enlever de la figure), qui :
A la fin du balayage, tous les pixels marqués 2 (à enlever de la figure) seront marqués 0 (dans le fond) :
Procédure : Amincissement séquentiel à mémoire
Pour le pixel p allant du premier au dernier, faire
si I(p) = 1 (p est dans la figure) et si le voisinage de p satisfait le critère,
alors I(p) := 2 (p est marqué à enlever de la figure et à rajouter au fond).
Pour tout pixel p, faire
si I(p) = 2,
alors I(p) := 0 (les pixels marqués à enlever de la figure sont enlevés).
Du point de vue algorithmique, la transformation des valeurs 2 en 0 à la fin d'une étape d'amincissement nécessite un balayage de l'image, et la répétition de ces balayages est un gaspillage de temps. Hilditch (1968) a proposé d'utiliser à chaque étape d'amincissement une nouvelle valeur pour les pixels marqués "à enlever de la figure", et qu'à l'issue de cette étape cette valeur soit logiquement identifiée à 0. On a donc la valeur fixe 1 pour un pixel non-enlevé de la figure, un ensemble f de valeurs de fond, et une valeur e pour les pixels à enlever de la figure, où e et f varient à chaque étape d'amincissement. On obtient ainsi :
Algorithme : Réduction séquentielle à mémoire
- Initialisation : f := {0} et e := 2.
- Répéter
jusqu'à ce que la figure ne change plus.
- Pour le pixel p allant du premier au dernier, faire
si I(p) = 1 et si le voisinage de p satisfait le critère,
alors I(p) := e,
- f := f
{e} et e := e +1.
- Finalisation :
Pour tout pixel p, faire
si I(p) > 1,
alors I(p) := 0.
Ainsi la valeur e d'un pixel indique non seulement qu'il a été enlevé de la figure, mais aussi que cela s'est passé lors de l'étape d'amincissement e - 1.