Les opérations morphologiques sont des filtres non-linéaires qui peuvent s'appliquer tant aux images binaires qu'à celles à niveaux de gris. Par exemple le filtre médian en fait partie. Nous allons décrire les 4 opérations morphologiques de base, à savoir la dilatation, l'érosion, l'ouverture et la fermeture, dans leur version pour les images binaires. Le document suivant décrira leur extension dite plate aux images à niveaux de gris.
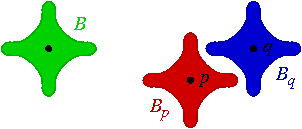
Contrairement à la plupart des mises en oeuvre pratiques de filtres, la fenêtre W(p) associée à un pixel p n'est pas nécessairement de forme rectangulaire ou circulaire. Au contraire, le choix de sa forme dépend du but recherché, plus particulièrement du type de structure qu'on veut mettre en évidence dans l'image. On choisit donc un ensemble B de pixels, appelé élément structurant, et la fenêtre W(p) associée à un pixel p sera le translaté de B positionné sur p, noté Bp.
|
Ci-contre : à gauche, l'élément structurant B, où la boule noire indique la position du point de référence ; à droite, au pixel p on associe la fenêtre W(p) = Bp obtenue en positionnant B sur p ; de même, au pixel q correspond la fenêtre W(q) = Bq. |
Soit X une figure, à savoir un ensemble de pixels. Pour un élément structurant B, la dilatation de X par B est l'ensemble obtenu en remplaçant chaque pixel p de X par sa fenêtre Bp :
DilB(X) =
{Bp | p
X}.
L'effet de la dilatation est d'abord d'élargir la figure, la hauteur et largeur de la figure dilatée seront les sommes respectivement des hauteurs et largeurs de la figure originelle et de l'élément structurant. Si l'élément structurant est décentré, la dilatation décalera la figure dans le même sens. Enfin les coins convexes de la figure seront déformés en fonction de l'élément structurant (par exemple si celui-ci est un disque, les coins convexes seront arrondis).
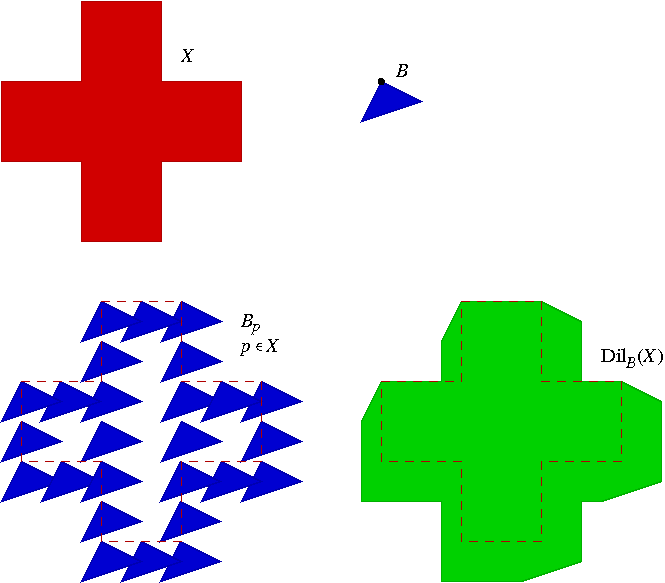
En haut à gauche, la figure X, et à droite, l'élément structurant B (la boule noire indiquant la position du point de référence). En bas à gauche, les fenêtres Bp pour un certain nombre de pixels p
Soit X une figure et B un élément structurant. L'érosion de X par B est l'ensemble des pixels p tels que la fenêtre Bp est incluse dans X :
ErosB(X) = {p | Bp
X}.
L'effet de l'érosion est d'abord de rétrécir la figure, la hauteur et largeur de la figure érodée seront les différences respectivement des hauteurs et largeurs de la figure originelle et de l'élément structurant (en particulier si l'élément structurant est plus large ou plus haut que la figure, l'érosion de celle-ci sera vide). Si l'élément structurant est décentré, l'érosion décalera la figure en sens inverse. Enfin les coins concaves de la figure seront déformés en fonction de l'élément structurant (par exemple si celui-ci est un disque, les coins concaves seront arrondis).
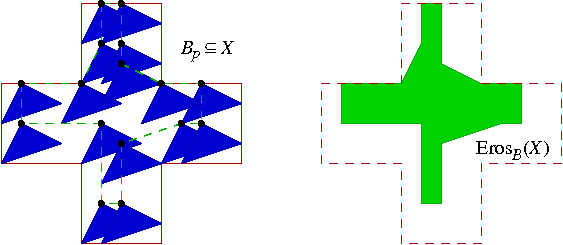
On considère les mêmes figure X et élément structurant B que plus haut. À gauche, plusieurs positions (boules noires) de pixels p dont les fenêtres Bp sont incluses dans X. À droite, l'érosion de X par B ; les coins concaves de la figure deviennent biseautés par les côtés du triangle B.
La dilatation et l'érosion ont des effets opposés sur une figure. Effectivement, dilater une figure revient à éroder son complément, mais cette érosion utilisera l'élément symétrique de celui de la dilatation.
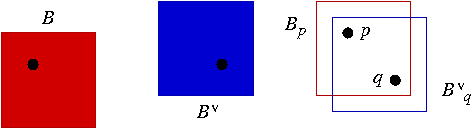
Soit Bv l'élément structurant obtenu en
appliquant à B une symétrie centrale par raport
à son point de référence. Pour un pixel
p, soit Bvp le translaté
de Bv positionné sur p ; alors les
fenêtres Bp et
Bvp sont duales dans le sens que
pour deux pixels p et q, on a q Bp si et
seulement si p Bvq, comme illustré
ci-dessous :
Pour une figure X, soit Xc = E \ X son complémentaire dans l'espace E. La dualité par complémentation entre la dilatation et l'érosion s'exprime ainsi :
ErosBv(X) = [DilB(Xc)]c et DilBv(X) = [ErosB(Xc)]c.
Nous illustrons ci-dessous la construction de l'érosion par dilatation du complémentaire :
On considère les mêmes figure X et élément structurant B que précédemment. À gauche, les éments structurants B et Bv. À droite, on associe à chaque pixel p
X
DilB(X),On définit l'ouverture par B comme la composition de l'érosion par B suivie de la dilatation par B :
OuvB(X) = DilB(ErosB(X)),
et la fermerture par B comme la composition de la dilatation par B suivie de l'érosion par B :
FermB(X) = ErosB(DilB(X)).
Ces deux opérations sont duales par complémentation, on a pour le symétrique Bv de B :
OuvBv(X) = [FermB(Xc)]c et FermBv(X) = [OuvB(Xc)]c.
L'ouverture de X par B est obtenue comme l'union de tous les translatés de B inclus dans X :
OuvB(X) =
Dualement, la fermeture de X par B est obtenue comme le complémentaire de l'union de tous les translatés de Bv inclus dans le complémentaire de X :
FermB(X) = [
En haut à gauche, les translatés de B inclus dans X, et à droite leur union donne l'ouverture de X par B. En bas à gauche, les translatés de Bv inclus le complémentaire de X, et à droite le complémentaire de leur union donne la fermeture de X par B.
L'ouverture élimine dans une figure toutes les parties plus étroites que l'élément structurant, et en déforme les coins convexes. Dualement, la fermeture rebouche toutes les parties du fond plus étroites que l'élément structurant, et déforme les coins concaves de la figure. Notons que le résultat de l'ouverture ou de la fermeture ne dépend pas de la position de l'élément structurant par rapport au point de référence.
Le bruit induit des changements aléatoires dans une figure, certains pixels de la figure passant au fond (faux négatifs), et certains pixels du fond passant à la figure (faux positifs). Ces erreurs forment généralement des agrégats de petite taille ; en prenant un élément structurant suffisamment grand, l'ouverture filtrera les faux positifs, tandis que la fermeture filtrera les faux négatifs. On appliquera donc ces deux opérateurs en succession (soit l'ouverture suivie de la fermeture, soit la fermeture suivie de l'ouverture) pour filtrer le bruit, comme nous l'illustrons ci-dessous :
Au milieu (en bleu), l'élément structurant B. En haut, à gauche la figure originelle X et à droite; la figure bruitée Y. Au milieu, à gauche l'ouverture OuvB(Y) et à droite la fermeture FermB(Y). En bas, à gauche la fermeture de l'ouverture FermB(OuvB(Y)) et à droite l'ouverture de la fermeture OuvB(FermB(Y)).
Plus l'élément structurant est grand, mieux le bruit sera éliminé, mais également plus la figure sera déformée (coins biseautés, parties étroites de la figure et du fond éliminées). Quand les parties étroites de la figure et du fond sont imbriquées, les deux opérateurs composés FermBOuvB et OuvBFermB donnent des résultats forts différents, comme le montre l'exemple suivant, dû à Pierre Soille :
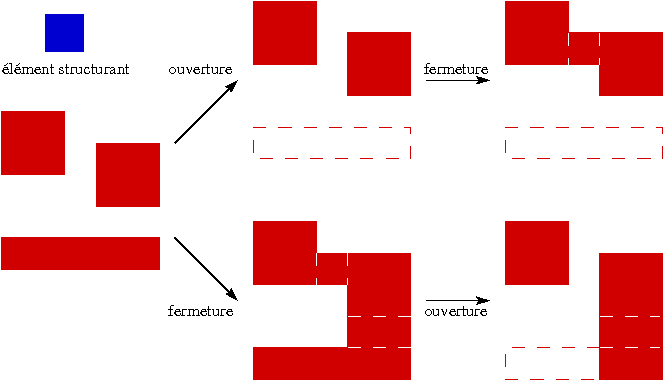
À gauche la figure originelle X (en rouge) et au-dessus l'élément structurant B (en bleu). On obtient : en haut l'ouverture OuvB(X) puis la fermeture de l'ouverture FermB(OuvB(X)), en bas la fermeture FermB(X) puis l'ouverture de la fermeture OuvB(FermB(X)) ; les pointillés indiquent la position de X.