d(p,q). En
d'autres termes, la pente de f est partout inférieure
ou égale à 1.
Un dégradé est une zone dans une image, où les niveaux de gris évaluent progressivement. En particulier, on peut considérer une image formant un dégradé sur tout l'espace où elle est définie ; nous appelons une telle image un dégradé global. Une technique classique pour créer un dégradé est le lissage linéaire. On peut essayer de créer un dégradé dans une zone d'une image en y plaquant les valeurs de niveaux de gris provenant d'un dégradé global. Nous considérons ici la génération d'un dégradé global à partir d'une image qui peut éventuellement être définie seulement sur une partie de l'espace. Notre méthode se base sur une légère modification de la transformée de distance.
Il faut d'abord caractériser mathématiquement la
progressivité des variations de niveaux de gris dans un
dégradé. Nous utilisons la condition de
Lipschitz. Soit E un espace muni d'une métrique
d ; alors une fonction f définie sur
E et à valeurs réelles (ou entières) est
de Lipschitz si et seulement si pour tous points p,q dans
E on a
|f(p) - f(q)| d(p,q). En
d'autres termes, la pente de f est partout inférieure
ou égale à 1.
Nous considérons les images définies sur un domaine ou masque S et à valeurs réelles. Soit R une partie de S appelée marqueur. Soit I une image partielle définie uniquement sur R (on peut avoir R = S, dans ce cas I n'est pas partielle). Selon Mc Shane (1934), la plus grande fonction de Lipschitz définie sur S et prenant sur R une valeur valeur inférieure ou égale à celle de I, est I+ définie sur S par
I+(p) = inf { I(q) + d(p,q) | q
R } .
Quand R est fini (par exemple si S l'est), cet "inf" devient un "min". Nous appelons I+ le dégradé inférieur de I. Son comportement est de "coller" autant que possible à I, tout en restant en dessous et avec une pente au plus 1 ; là où I monte trop vite, ou n'est pas définie, I+ montera avec une pente 1. Nous illustrons ci-dessous I+ dans le cas d'un masque unidimensionnel S :
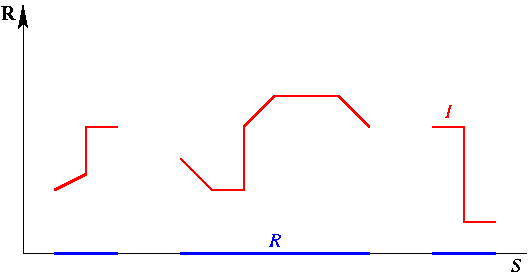
En bleu, le marqueur R, et en rouge, l'image I
définie sur R.
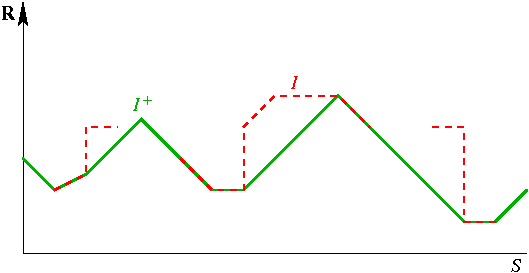
En vert, le dégradé inférieur
I+.
Un cas particulier est donné par I valant identiquement 0 sur R : dans ce cas I+ est la transformée de distance de R :
I+(p) = inf { d(p,q) | q
Dualement, on obtient le dégradé supérieur I¯ par la succession d'un négatif (inversion des niveaux de gris), du dégradé inférieur, puis d'un nouveau négatif :
I¯ = N(N(I)+).
On a alors
I¯(p) = sup { I(q) - d(p,q) | q
Quand R est fini (par exemple si S l'est), ce "sup" devient un "max". Le comportement de I¯ est le dual de celui de I+, à savoir de "coller" autant que possible à I, tout en restant au dessus et avec une pente au plus 1 ; là où I descend trop vite, ou n'est pas définie, I¯ descendra avec une pente 1. Nous illustrons ci-dessous I¯ dans le cas d'un masque unidimensionnel S :
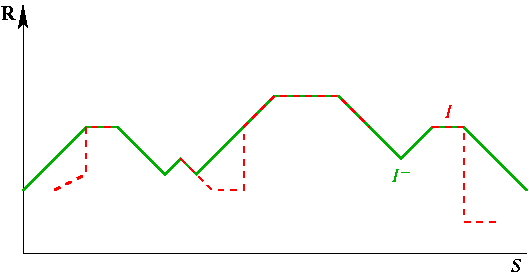
En vert, le dégradé supérieur
I¯.
Sur S \ R (là où I n'est pas définie), I+ crée un pic, tandis que I¯ crée un creux. Un comportement plus équilibré sera obtenu en prenant la moyenne (I+ + I¯) / 2, comme illustré ci-desous :
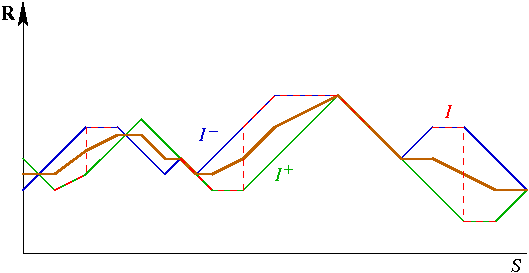
En rouge pointillé, l'image I ; en vert, le
dégradé inférieur I+ ;
en bleu, le dégradé supérieur
I¯ ; en brun la moyenne des deux.
Lorsque le domaine S est une grille rectangulaire dans Z2 et d est une distance de chanfrein satisfaisant les conditions de Montanari, on peut calculer I+ et I¯ au moyen d'une modification de l'algorithme séquentiel de transformée de distance comportant trois étapes (initialisation, balayage dans l'ordre direct, balayage dans l'ordre inverse).
Pour le calcul de I+, on modifie l'initialisation comme suit :
f(p) := I(p) si p
f(p) := H si p
où H est un nombre considéré comme "infini". Ensuite on procède aux deux étapes de balayage dans l'ordre direct puis dans l'ordre inverse, et à la fin la fonction f donne I+.
Pour le calcul de I¯, l'initialisation est modifiée comme suit :
f(p) := I(p) si p
f(p) := -H si p
Ensuite dans l'étape de balayage dans l'ordre direct l'affectation
f(p) := min { f(q) + M¯p(q) | q dans V¯(p) }.
est remplacée par
f(p) := max { f(q) - M¯p(q) | q dans V¯(p) }.
De même, dans l'étape de balayage dans l'ordre inverse l'affectation
f(p) := min { f(q) + M+p(q) | q dans V+(p) }.
est remplacée par
f(p) := max { f(q) - M+p(q) | q dans V+(p) }.
Ainsi à la fin la fonction f donne I¯.