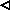 on E correspond as
follows:
on E correspond as
follows:
One calls an ``Alexandrov topology'' a topological space where an arbitrary intersection of open sets is open, or equivalently, every point has a least neighbourhood. Alexandrov called it a ``discrete space''.
The Alexandrov specialization theorem characterizes an Alexandrov
topology in terms of a quasi-order, that is, a reflexive and
transitive relation on that space. An Alexandrov topology on E and a
quasiorder 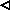 on E correspond as
follows:
on E correspond as
follows:
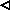 q iff p belongs to the
closure of {q};
q iff p belongs to the
closure of {q};
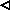 , that is, sets X with (p
, that is, sets X with (p 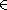 X, p
X, p 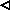 q) implies
(q
q) implies
(q 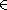 X).
X).
Moreover that quasiorder is an order relation (i.e., it is antisymmetric) iff the topology satisfies the T0 separation axiom.
The usual reference for this result is [2], as well as Alexandrov's later works (such as his topology book with Hopf, or his monograph on combinatorial topology).
In fact, while developing his theory, Alexandrov discussed with Birkhoff. In [1] Alexandrov proposed the axioms for a ``discrete space'' and stated that it corresponded to a partially ordered set. Birkhoff answered him in [3], and among other things stated that he was studying similar structures in the framework of abstract algebra. Then Alexandrov published his results in [2], in particular the specialization theorem. The same year Birkhoff published [4], where he proved that a ``complete ring of sets'' (family of sets closed under arbitrary union and intersection, including void ones) corresponds to a quasiorder. A ``complete ring of sets'' means exactly the same thing as ``Alexandrov topology'', and the quasiorder given by Birkhoff is the same as the one given by Alexandrov, but in another wording.
Birkhoff showed also that the ``complete ring of sets'' is a ``complete field of sets'' (the family is also closed under complementation) iff the quasiorder is an equivalence relation (i.e., it is symmetric); in topological terms, it means that the open sets coincide with the closed sets.
Therefore the specialization theorem attributed to Alexandrov is in some way also due to Birkhoff.
[1] Paul Alexandrov, Sur les espaces discrets, Comptes Rendus de
l'Académie des Sciences 200 (1935), 1469-1471.
[2] Paul Alexandrov, Diskrete Räume, Mat. Sb. 2 (1937), no. 44,
501-519.
[3] Garrett Birkhoff, Sur les espaces discrets, Comptes Rendus de
l'Académie des Sciences 201 (1935), 19-20.
[4] Garrett Birkhoff, Rings of sets, Duke Math J. 3 (1937), no. 3,
443-454.
March the 29th, 2007
Christian Ronse